This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
56 solutions
best method
Simple sir. It is cross multiplication. Problem is very lucidly solved by Doug Neal.
7^{x+1}+7^{x-1}=7^2+7^0 x+1=2 x=1
how we get 7^x =7
Log in to reply
Because 50 we knew that is answer and the 7x is the term useless so that in our mind ,we need to delete it
We divide both sides of the equation with 50 and multiply both sides of the equation with 7.
You put the reciprocal of 50/7 on the right side to get only 7^x on one side.
Wow Doug Neal, you sure paid attention in algebra class....great math skill.
quite nice!!!!
Best method
Nice work Doug,I hope I can wory my way up with.Help from Great minds like yourself.
7^2(7^x-1)+7^x-1=50 (49+1)(7^x-1)=50 7^x-1=1 Ln base 7 on both sides X-1=0 X=1
Will u please explain why 50 is gone in the proess?
Log in to reply
when we take 50 /7 another side 7 goes up and 50 down so we can cut 50 and 50 ,7 is left
To remove 50/7 from the left hand side, both sides are divided by that number. Within the equation, this will happen:
50÷(50/7)
= 50×(7/50)
By utilising the cross-multiplication method, the number 50 is removed and 7 is left
in the 4th step as both the sides of the equation contain 50..50 got cancelled..
how we get 7^x=7
Nice method
can you also use logarithms to figure this equation out?
7 x + 1 + 7 x − 1 = 5 0
7 x + 1 + 7 x − 1 = 7 2 + 7 0
x + 1 + x − 1 = 2
2 x = 2
x = 1
Fastest way yo do it. Nice one!!
7 x + 1 + 7 x − 1 = 7 x − 1 ( 7 2 + 1 ) = 5 0 ∗ 7 x − 1 = 5 0 ⇒ x − 1 = 0 , x = 1
I think There should be x − 1 = 0 instead of x − 1 = 1
Marvelous solution....
VEry good indeed
This solution is much comprehensive. No more using of logarithm. Very algebraic!
Here is an arguably more intuitive and efficient way to solve this problem at a glance.
You know that the difference between 7 x + 1 and 7 x − 1 is 7 2 because:
( x + 1 ) − ( x − 1 ) = 2 thus,
7 2 = 4 9
So the only way for 7 x + 1 + 7 x − 1 = 5 0 is if
7 x − 1 = 1
Therefore:
x − 1 = 0
x = 1
I don't get where you are going with difference between 7 x + 1 a n d 7 x − 1 i s 7 2 . you seem to imply by that statement that 7 x + 1 − 7 x − 1 = 7 2 - that is not the case - exponents don't work like that.
Log in to reply
He is trying to say that 7 x − 1 × 7 2 = 7 x − 1 + 2 , which = 7 x + 1
So if you factor out the 7 x − 1 from the left-hand side, you get 7 x − 1 ( 7 2 + 1 ) = 5 0 which if simplified ends up being 7 x − 1 = 1
good going mate
That's how you do it..!! Cheers.
7^x+1^ + 7^x-1^ = 50
7^x^ * 7 + 7^x^/7 = 50
7^x ^(7 + 1/7) = 50
7^x^ * 50/7 = 50
7^x^ = 7^1^
X = 1
It's really simple. If you know that 7 to the power of 2 is 49, then obviously you have to add 1 more to 49. So if you plug in 1 for x, then you get 7 to the power of 2 (49) + 7 to the power of 0 (1) which equals 50!
Youngest person with easiest explanation, good job. This is how I solved it as well. Like the way you do math.
7^(x +1) + 7^(x-1) =50
or, 7^x . 7 + 7^x . 1/7=50
or, 7^x( 7 + 1/7 )=50
or, 7^x . 50/7 =50
or, 7^x = 7 ^1
or, x =1
You could use logs but honestly I just guessed and checked. Worked great.
Why do people not check their work in case of any extraneous solutions were found? Also, how many would have solved it like how I did?
how about this one?:)
7^x+1 + 7^x-1 = 50
[(x+1) + (x-1)]log(7) = log(50)
2x = log(50)/log(7)
x = 1
7^(x+1) + 7^(x-1) = 50
7^(x-1) (7^2 + 1) = 50
7^(x-1) = 1
x - 1 = 0
x = 0
Another solution
7^(x+1) + 7^(x-1) = 50
7^(x+1) + 7^(x-1) = 49 + 1
7^(x+1) + 7^(x-1) = 7^2 + 7^0
x+1 = 2 and x-1 = 0
Then
x = 1
A very simple problem. 7 ^(x+1)+ 7^(x-1). x=1 7^(1+1) + 7^ (1-1)= 49+1=50. I am surprised that no other kids can solve this, only adults.
7 x + 1 + 7 x − 1 = 5 0 ⟹ 7 2 × 7 x − 1 + 7 x + 1 ⟹ ( 4 9 + 1 ) 7 x − 1 = 5 0 ⟹ 5 0 × 7 x − 1 = 5 0 ⟹ 7 x − 1 = 1
⟹ 7 x − 1 = 7 0 ⟹ x − 1 = 0 ⟹ x = 1
- 7 x + 1 + 7 x − 1 = 5 0
- 7 x ⋅ 7 + 7 x ⋅ 7 − 1 = 5 0
- 7 x ( 7 + 7 − 1 = 5 0
- 7 x ⋅ 7 5 0 = 5 0
- 7 x ⋅ 7 1 = 1
- 7 x − 1 = 7 0 x − 1 = 0 , x = 1
Get coefficients
No one likes a fraction there
Divide 50 and solve power
7^x+1 + 7^x-1 = 50 7^x+1 + 7^x-1 = 7^2 + 7^0 (x+1)+(x-1)=2 + 0 2x = 2 x=1
7^0=1 ,7^1=7, 7^2=49 then: 1 + 49=50
Divid expression by 7 so 7^(x +1)\7+7^(x -1)\7=50\7,,,7^(x+1-1)+7^(x-2)=50\7,,,,,,,,, 7^x+7^(x)×7^-2=50\7,,7^x×(1+7^-2)=50\7,,7^x×(50\7^2)=50\7,,7^x=7^1,,,x=1###
7^(x-1)(7^2 +1) = 50 7^(x-1)(50) = 50 7^(x-1) = 1 x-1 = 0, because 7^0=1 Therefore x = 1
7^(x+1) + 7^(x-1) =50
Solving the exponent
(x+1)(x-1)
x^2 - 1^2
x=√1
x=1
7^(x+1)+7^(x-1)=50
7^(x+1)+7^(x-1)=7^2+7^0
Equating differently
7^(x+1)=7^2 or 7^(x-1)=7^0
=>(x+1)=2 or (x-1)=0
=>x=1
(7^x.7^1) +(7^x/7^1) = 50 |.7
(7^x.7^2) +(7^x) = 350
(7^x)(7^2 + 1) = 350
7^x (50) = 350
7^x = 350/50
7^x = 7^1
x = 1
7 x + 1 + 7 x − 1 = 5 0
7 x − 1 ( 7 2 + 1 ) = 5 0
7 x − 1 ( 4 9 + 1 ) = 5 0
7 x − 1 × 5 0 = 5 0
7 x − 1 = 1
7 x − 1 = 7 0
x − 1 = 0
x = 1
(7^x+1)+(7^x-1)=50
OR(7^x)*7 + (7^x)/7=50
OR(7^x)(7+1/7)=50
OR(7^x)(50/7)=50
OR 7^x=50*7/50=7=7^1
Therefore, x=1
Call 7^{x+1} = y; And remember that 7^{x-1} = 7{(x+1) -1 -1} = 7^{x+1} \times 7{-2}; So, 7^{x+1} + 7^{x-1} = 50 it's the same thing of y + y \times 7{-2} = 50; y = 49; If 7^{x+1} = y; Then, 49 = 7^{x+1}; 49 = 7^{2} = 7^{x+1}; x+1 = 2; x = 1.
7^(x+1) + 7^(x-1) = 50 so
7^(x+1) + 7^(x-1) = 49 + 1
rewriting the expression with 7 as its base:
7^(x+1) + 7^(x-1) = 7^2 + 7^0
By properties of exponential function
(x+1)+(x-1) = 2+0
x+x+1-1=2
2x=2
x=1
7^(x+1) +7^(x-1)=7^2 +7^0
x+1+x-1 =2+0
2x =2
x=1
Do we have some other method to solve this problem
X+1=2 x-1=1. 7x7=49+1=50, so X=1
{ 7 }^{ x+1 }={ 7 }^{ x }X7\ 7^{ x-1 }=\frac { { 7 }^{ x } }{ 7 } \ \ { 7 }^{ x }(7+\frac { 1 }{ 7 } )=50\ { 7 }^{ x }=7\quad \quad (7+1/7=50/7)\ x=1
7^{x+1} + 7^{x-1} = 50
this can be written as
7^{x+1} + 7^{x-1} = 7^{2} + 7^{0}
7^{x+1} + 7^{x-1} = 7^{1+1} + 7^{1-1}
So, x = 1
7^(x+1)+7^(x-1)=50 or, 7^x(7+1/7)=50 or, 7^x*(50/7)=50 or, 7^x=7=7^1 or, x=1
Am i the only one one who just thought "hey 7^2=49 7^0 =1 49+1= 50 !" 7^2 = 7^ 1 +1 = 49 7^0 =7^ 1 -1 = 1
This method is more applicable to a wider range of problems:
7 2 x = 5 0 2 x × l n 7 = l n 5 0 2 x = l n 7 l n 5 0 x = 1
Moderator note:
How did you get the first line?
7 x − 1 + 7 x + 1 = 7 2 x
Instead, what we have is 7 x − 1 × 7 x + 1 = 7 2 x .
Ok, I think I cheated, used logic rather than math. I know 7^2 is 49, very near to the solution. So I thought it might help if I write 50 as terms that involve 7 to a certain power. 50=49+1=7^2+7^0. Well if I look to the other side, it is extremely easy make the exponents equal 2 and 0. So x must be 1.
7 x + 1 + 7 x − 1 = 7 2 +1
7 x + 1 + 7 x − 1 = 7 2 + 7 0
by analogy it's very clear that x = 1
or
7 × 7 x + 7 7 x = 5 0
7 x × ( 7 + 7 1 ) = 5 0
7 x × ( 7 5 0 ) = 5 0
5 0 × 7 x − 1 = 5 0
7 x − 1 = 1
L o g 7 ( 7 x − 1 ) = L o g 7 ( 1 )
x − 1 = 0
x = 1
7^(x+1)+7^(x-1)=50
>7^x*7+7^x / 7=50 >let 7^x =a then the equation is simply
>7 a + a / 7 =50 >(49+1)a / 7 = 50 >50 a / 7 = 50 >a = 7
>putting the value of a = 7^x we find >7^x = 7 >x = 1 (using exponential rule : if a^x = a^b then x = b)
The t possibilities for getting 50 with powers of 7 are just with 7 power 0, 7 power 1, and 7 power 2. Logically 7 power 0 + 7 power 2 gives the result, as 49+1 = 50. now equate it as x+1=2 and x-1=0. You will get answer as 1.
I have directly put the value x=1 because it is simple. Only you have to find the relation in between 7 and 50 such as
50 = 49 +1
Since 49 = square of 7 then we have to put only 1 and we can get the answer.
7^x+1 +7^x-1=50 7^2x=50 49x=50 X=50-49 X=1
This is a case of converting the number bases.
Since the left hand side is only in the form of sum of powers of 7 , this leads me to convert the number 5 0 to base 7 .
Listing down the first few powers that don't exceed 5 0 , we have 7 0 = 1 , 7 1 = 7 , 7 2 = 4 9 , in which case we can see that 4 9 + 1 = 5 0 or 7 2 + 7 0 = 5 0
So we compare: x + 1 = 2 , x − 1 = 0 which gives x = 1
now we know we can take 7^2 + 7^0=49+1=50 so if we take x as 1 then 1+1=2 and 1-1=0 SOLVED......
7^(x+1)+7^(x-1)=50
=> 7^x.7+7^x/7=50
=> 7^x (7+1/7)=50
=> 7^x(50/7)=50
=> 7^(x-1)=1
=> x-1 = 0
=> x = 1
7 x + 1 + 7 x − 1 = 7 x 7 1 + 7 x 7 − 1 = 7 x ( 7 + 7 1 ) = 5 0
Rewrite 7 + 7 1 as 7 4 9 + 7 1 = 7 5 0 :
Therefore 7 x ( 7 5 0 ) = 5 0
⇒ 7 x = 7 ⇒ x = 1
Wow, this is the most simple solution so far
7^x-1(7^2 + 1) = 50 7^x-1(50) = 50 7^x-1(50)/50 = 50/50 7^x-1 = 1 7^x-1 = 7^0 x-1 = 0 x = 1
7^x(7+1/7)=50 7^x(50/7)=50 7^x=7 Xlog7=log7 X=1
(X+1)+ (x-1)= 7^2+1=7^2+7^0 2x=2+0=2. Hence x=1.
its logic.... (x+1)-(x-1)=2 7^2=49 x=2
Yeah, but hit and trial doesn't work everytime, especially on Brilliant. Think it the other way, if I would've given this problem as a Multiple Choice one with similar options??
7^x(7+1/7) =50
7^x(50/7)=50
7^x=7
Hence x=1
50 = 49 - 1, 50 = 7^2 + 7^1, if 7^(x+1)+7^(x-1)=50, then x+1=2 and x=1
Suppose 7^x=a then a/7 +7a=50 => a/7 + (49a)/7=50 => 50a=350 => a=7 => 7^x=7 => x=1
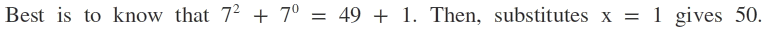

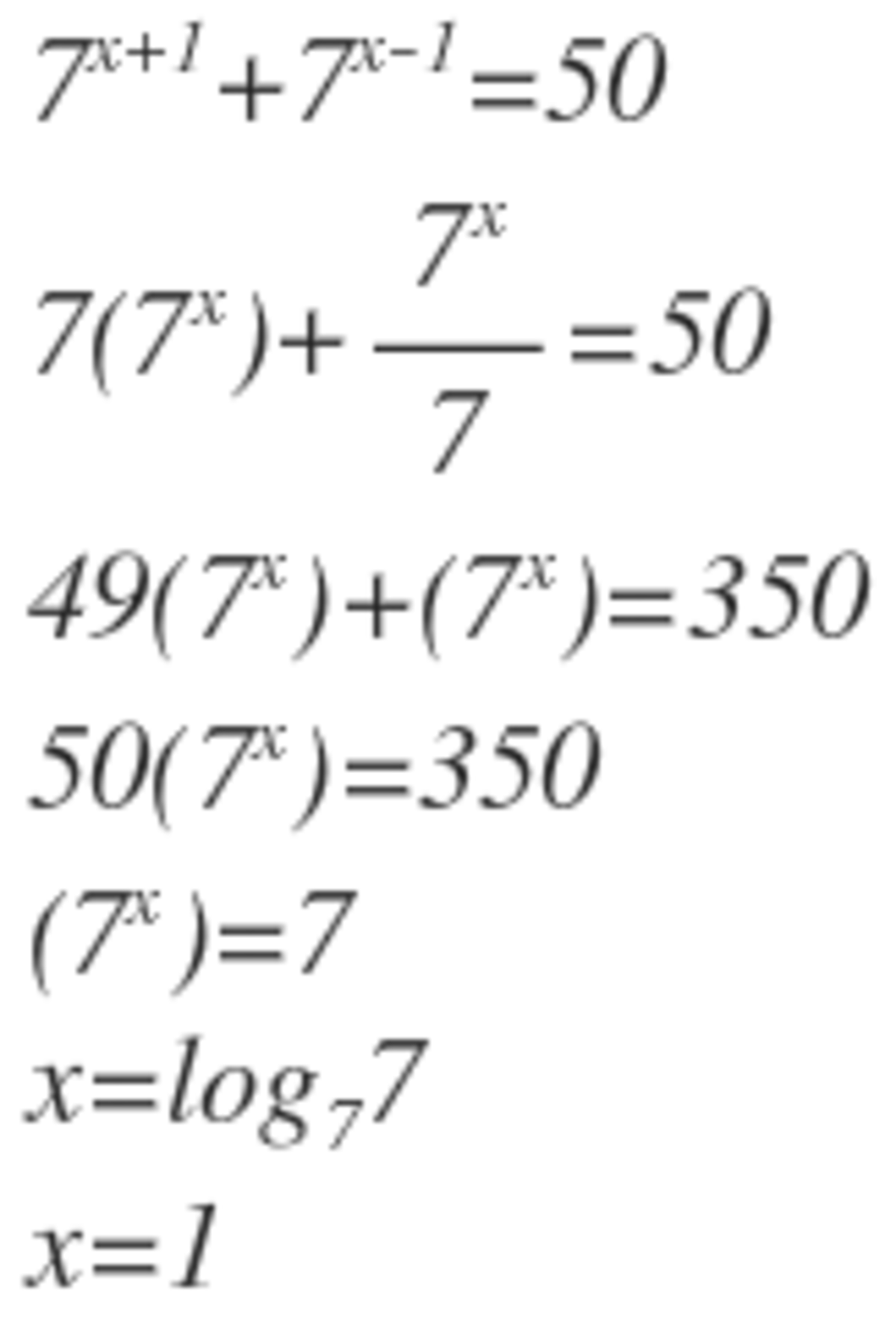
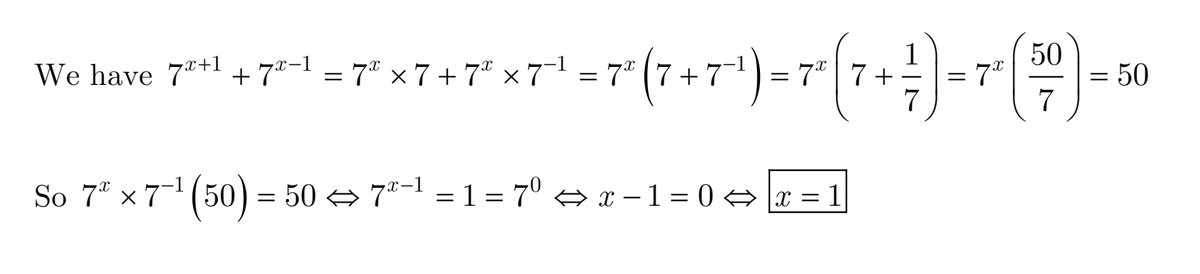
7 x + 1 + 7 x − 1 = 5 0 7 x × 7 + 7 7 x = 5 0 7 x ( 7 + 7 1 ) = 5 0 7 x ( 7 5 0 ) = 5 0 7 x = 7 x = lo g 7 7 x = 1