Trig or treat
Geometry
Level
5
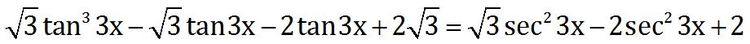 Find the sum of the first 3 lowest positive values of x in degrees.
Find the sum of the first 3 lowest positive values of x in degrees.
The answer is 65.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
the main problem with this problem is that it looks tremendously horrible at first sight. i cannot find any good method to solve this. if you have, please do comment
First we write 3 x = Z .. (for simplicity, obviously)
then we write s e c 2 Z = 1 + t a n 2 Z , bring all the terms to the L.H.S, group them, to get our equation:
3 t a n 3 Z + ( 2 − 3 ) t a n 2 Z − ( 2 + 3 ) t a n Z + 3 = 0
From here, it is very easy to observe that t a n Z = 1 satisfies the equation.
Thus, by good-ol' factorisation again and again, we get :
( t a n Z − 1 ) ( t a n Z + 3 ) ( t a n Z − 3 1 ) = 0
From there, calculation yields the 3 lowest positive values of x as:
x = 1 0 ∘ , 1 5 ∘ , 4 0 ∘
Our sum = 6 5