Trig Wig

From our initial equation, $\sin^2{\theta} = \dfrac{75 \cos^3{\theta} - 1}{2}$ . Using the Fundamental Theorem, we have $\left ( \dfrac{75 \cos^3{\theta} - 1}{2} \right ) + \cos^2{\theta} = 1 \Leftrightarrow 75 \cos^3{\theta} + 2 \cos^2{\theta} - 3 = 0$ .

This equation has roots $\cos{\theta} = \dfrac{1}{3}$ or $\cos{\theta} = \dfrac{-9 \pm \sqrt{-219}}{50}$ , and so we will restrain to $\cos{\theta} = \dfrac{1}{3}$ .

The result yields $\sin{\theta} = \pm \dfrac{\sqrt{8}}{3}$ and thus $\tan{\theta} = \pm \sqrt{8}$ . This leads to the answer as $3 + 4 \cdot 8^2 = \boxed{259.}$

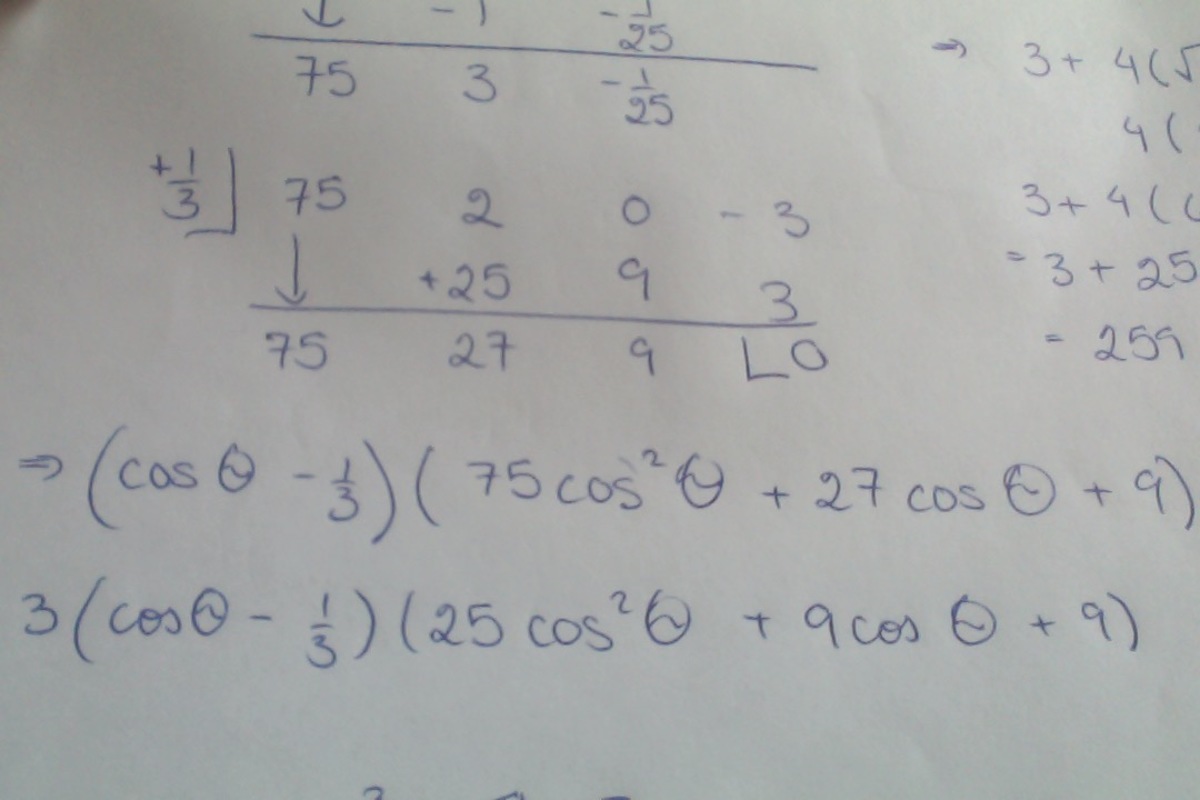
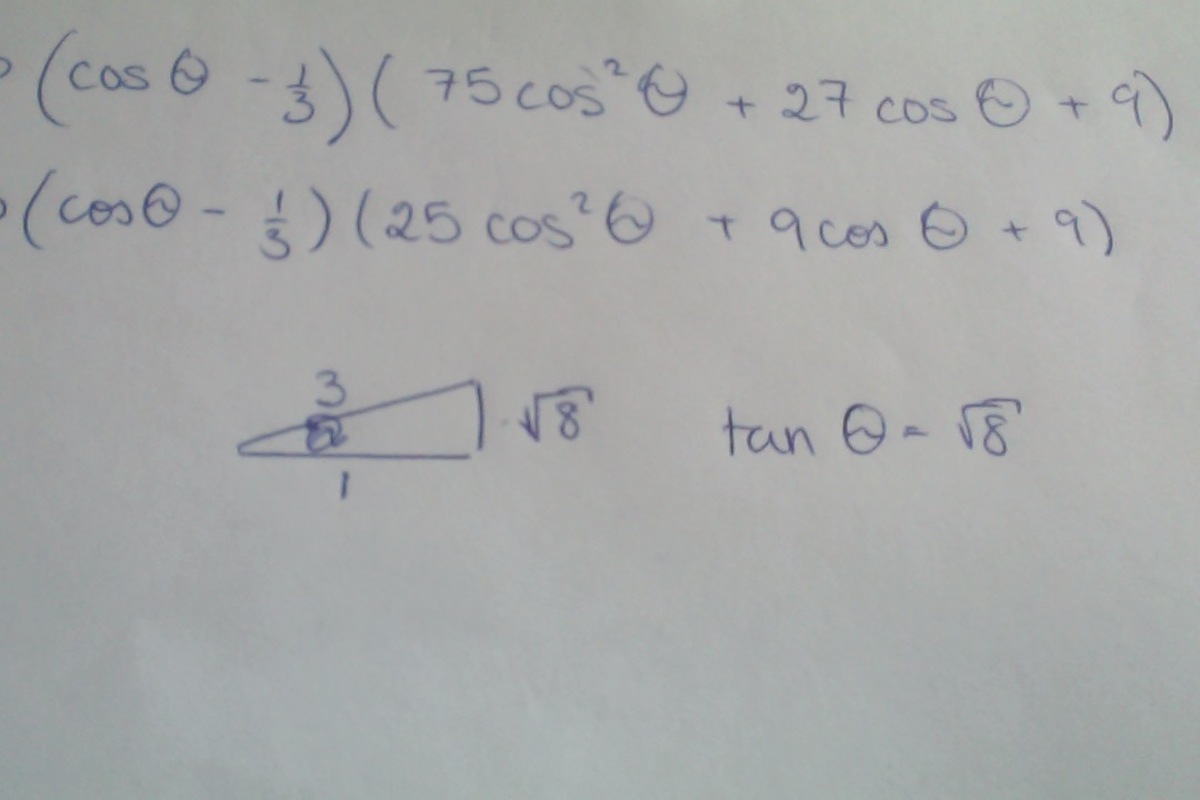
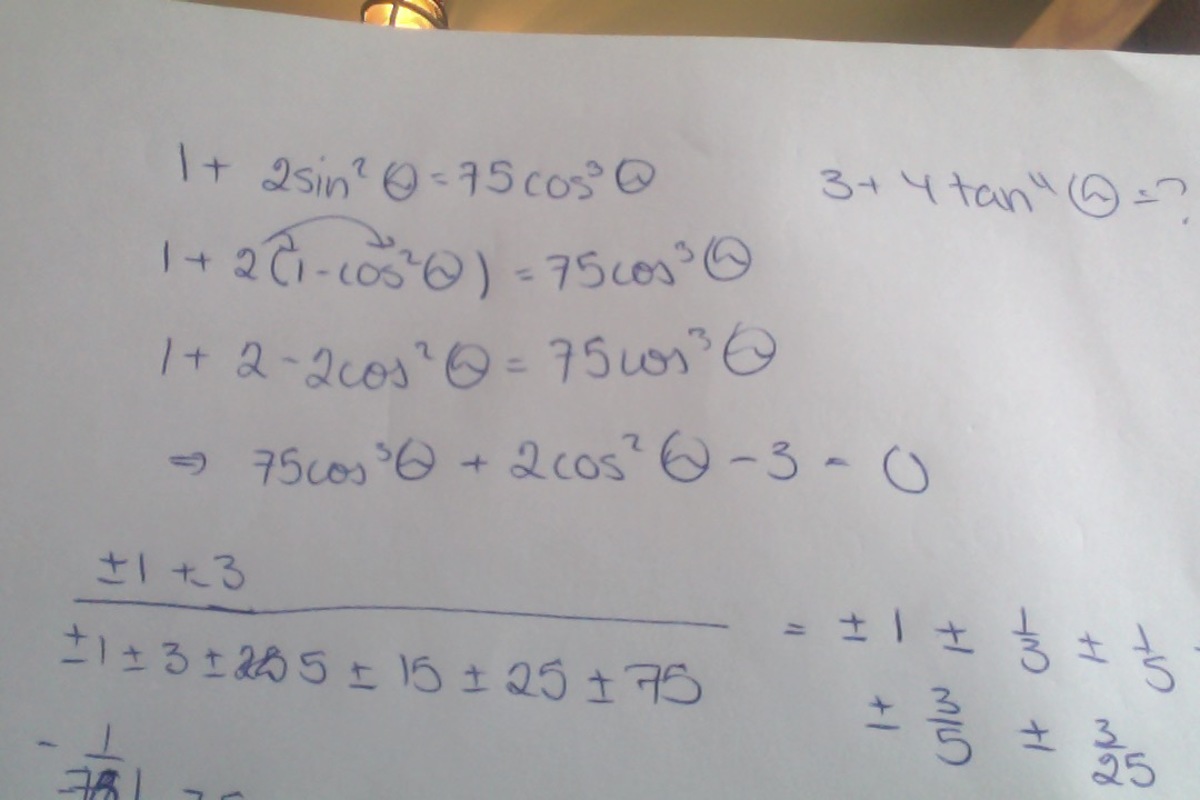
To solve this, I re-wrote the expression in terms of cosine (see pictures), and I used synthetic division (rational roots theorem). Once I found root of the equation, I solved for tangent and substituted into the equation and got 259.