Trig?
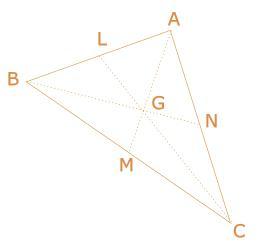 L, M and N are the midpoints of the sides AB, BC and CA of
ABC.
AM, BN and CL intersect at G.
L, M and N are the midpoints of the sides AB, BC and CA of
ABC.
AM, BN and CL intersect at G.
If AM units and GM units, then what is the length of AG?
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Well, there is a theorem stating that a line joining a midpoint of one side of a triangle and the centriod of the triangle has a measurement of 3 1 of the measurement of the line joining the midpoint of the same side of the triangle and it's opposite vertex.
So, we get:
5 x − 3 x + 2 = 3 1
3 x + 6 = 5 x − 3
2 x = 9
x = 4 . 5
Getting the difference between AM and Gm, we get:
5 x − 3 − ( x + 2 ) ⇒ 4 x − 5 ⇒ 4 ( 4 . 5 ) − 5 ⇒ 1 8 − 5 = 1 3
There.