Sine Sine Cosine Cosine, I got it!
If x and y are acute angles such that
sin y sin x = 2 1 , cos y cos x = 2 3 ,
what is tan 2 ( x + y ) ?
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Summing the equations we get
sin y sin x + cos y cos x = 2 1 + 2 3 ⇒ sin y cos y sin x cos y + sin y cos x = 2 that is sin x cos y + sin y cos x = 2 sin y cos y hence we land on the v e r y n i c e equation sin ( x + y ) = sin ( 2 y ) Since 0 ∘ < x , y < 9 0 ∘ , both x + y and 2 y are in the ( 0 ∘ , 1 8 0 ∘ ) range and the above equality then implies x + y = 2 y OR x + y = 1 8 0 ∘ − 2 y if x + y = 2 y we'd get x = y and sin y sin x = 1 against the first equality in our assumptions. So necessarily we have x + y = 1 8 0 ∘ − 2 y ⇒ x = 1 8 0 ∘ − 3 y As consequence we have two nice facts. The first is
sin y sin ( 1 8 0 ∘ − 3 y ) = 2 1 ⇒ sin y sin ( 3 y ) = sin y sin ( 2 y ) cos y + cos ( 2 y ) sin y = 2 1 and so 2 cos 2 y + 2 cos 2 y − 1 = 4 cos 2 y − 1 = 2 1 ⇒ cos y = 8 3 that also means sin y = 8 5 (in derivinq these values we used the fact that 0 < y < 9 0 ∘ so both sin y and cos y are positive).
The second thing is
tan ( x + y ) = tan ( 1 8 0 ∘ − 2 y ) = − tan ( 2 y ) = = tan 2 x − 1 2 tan y = 3 5 − 1 2 3 5 = 3 2 2 3 5 = 3 3 5 = 1 5
hence
tan 2 ( x + y ) = 1 5
To save time and space, let's use s,c and t to stand for sin, cos and tan.
The first equation gives
s x = 2 s y … ( 1 )
and the second equation gives
c x = 2 3 c y … ( 2 )
Squaring these equations and adding gives
4 s 2 y + 4 9 c 2 y = 1
From this it follows easily that
s 2 y = 8 5
and so
c 2 y = 8 3
Now using equations (1) and (2) it is easy to find
s 2 x = 3 2 5
c 2 x = 3 2 2 7
Using these last four equations we can find
t 2 y = 3 5
t 2 x = 2 7 5
Using these last two equations in the standard formula for tan ( x + y ) gives
t 2 ( x + y ) = ⎝ ⎛ 1 − 3 5 2 7 5 3 5 + 2 7 5 ⎠ ⎞ 2
After a couple of lines of careful arithmetic this simplifies to 1 5

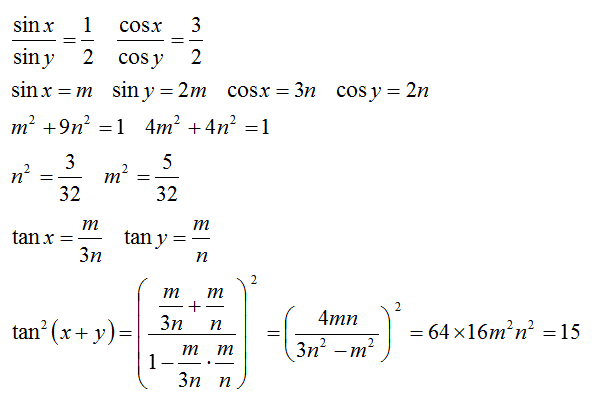
It is given that:
⎩ ⎪ ⎨ ⎪ ⎧ sin y sin x = 2 1 cos y cos x = 2 3 ⇒ sin y = 2 sin x ⇒ cos y = 3 2 cos x . . . ( 1 ) . . . ( 2 )
⎩ ⎨ ⎧ E q . 1 2 : E q . 2 2 : ⇒ sin 2 y = 4 sin 2 x ⇒ cos 2 y = 9 4 cos 2 x . . . ( 1 a ) . . . ( 2 a )
E q . 1 a + E q . 2 a : ⇒ 1 = 4 sin 2 x + 9 4 cos 2 x × cos 2 x 1 : ⇒ 4 tan 2 x + 9 4 = sec 2 x = 1 + tan 2 x ⇒ 3 tan 2 x = 9 5 ⇒ tan x = 9 1 5
E q . 2 E q . 1 : ⇒ tan y = 3 tan x
tan ( x + y ) = 1 − tan x tan y tan x + tan y = 1 − 3 tan 2 x 4 tan x = 1 − 8 1 4 5 9 4 1 5 = 3 6 3 6 1 5 = 1 5
Therefore, tan 2 ( x + y ) = 1 5