Trigonometric Bases
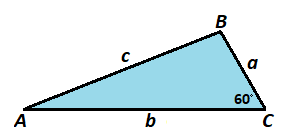
Archeologists have recently discovered evidence that the fictitious lost civilization of Brilliantica used a type of trigonometric ratio that used triangles with 6 0 ° angles and 1 2 0 ° angles instead of 9 0 ° angles. For example, for △ A B C below, where C is a 6 0 ° angle, sin 6 0 ° A = c a , cos 6 0 ° A = c b , tan 6 0 ° A = b a , sin 6 0 ° B = c b , cos 6 0 ° B = c a , and tan 6 0 ° B = a b .
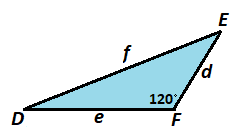
Likewise, for △ D E F below, where F is a 1 2 0 ° angle, sin 1 2 0 ° D = f d , cos 1 2 0 ° D = f e , tan 1 2 0 ° D = e d , sin 1 2 0 ° E = f e , cos 1 2 0 ° E = f d , and tan 1 2 0 ° E = d e .
What can cos 6 0 ° 3 x + cos 1 2 0 ° 3 x (for 0 < x < 6 0 ° ) be simplified to?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice approach! Thanks for sharing your solution!
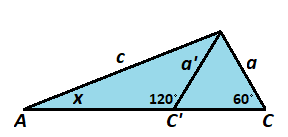
Let ∠ A = x , ∠ C = 6 0 ° , and c = 1 . Then a = sin 6 0 ° x and b = cos 6 0 ° x , and by law of cosines, sin 6 0 ° 2 x − sin 6 0 ° x cos 6 0 ° x + cos 6 0 ° 2 x = 1 , so cos 6 0 ° 3 x + sin 6 0 ° 3 x = ( cos 6 0 ° x + sin 6 0 ° x ) ( sin 6 0 ° 2 x − sin 6 0 ° x cos 6 0 ° x + cos 6 0 ° 2 x ) = cos 6 0 ° x + sin 6 0 ° x .
Let ∠ A = x , ∠ C ’ = 1 2 0 ° , and c = 1 . Then a ’ = sin 1 2 0 ° x and b ’ = cos 1 2 0 ° x , and by law of cosines, sin 1 2 0 ° 2 x + sin 1 2 0 ° x cos 1 2 0 ° x + cos 1 2 0 ° 2 x = 1 , so cos 6 0 ° 3 x − sin 6 0 ° 3 x = ( cos 6 0 ° x − sin 6 0 ° x ) ( sin 6 0 ° 2 x + sin 6 0 ° x cos 6 0 ° x + cos 6 0 ° 2 x ) = cos 6 0 ° x − sin 6 0 ° x .
Also, a and a ’ are sides of an equilateral triangle, so a = a ’ or sin 6 0 ° x = sin 1 2 0 ° x .
Therefore,
cos 6 0 ° 3 x + cos 1 2 0 ° 3 x
= cos 6 0 ° 3 x + sin 6 0 ° 3 x + cos 1 2 0 ° 3 x − sin 1 2 0 ° 3 x
= cos 6 0 ° x + sin 6 0 ° x + cos 1 2 0 ° x − sin 1 2 0 ° x
= cos 6 0 ° x + cos 1 2 0 ° x .
Let the Brilliantica's hypotenuse A B = 1 , then cos 6 0 ∘ x = A D and cos 1 2 0 ∘ x = A C . We note that △ B C D is equilateral. Since B E = sin x , B C = C D = D B = 3 2 sin x and C E = E D = 3 1 sin x . Then we have:
⎩ ⎪ ⎨ ⎪ ⎧ cos 6 0 ∘ x = A D = A E + E D = cos x + 3 sin x cos 1 2 0 ∘ x = A C = A E − C E = cos x − 3 sin x
Then cos 6 0 ∘ x + cos 1 2 0 ∘ x = 2 cos x . Now we have:
cos 6 0 ∘ 3 x + cos 1 2 0 ∘ 3 x = ( cos x + 3 sin x ) 3 + ( cos x − 3 sin x ) 3 = 2 cos 3 x + 2 sin 2 x cos x = 2 cos x ( cos 2 x + sin 2 x ) = 2 cos x = cos 6 0 ∘ x + cos 1 2 0 ∘ x