Trigonometric Integral

Considering the function $f$ , we see that $\begin{array}{rcl} tf'(t) & = & \displaystyle t \int_0^{2\pi} e^{t\cos\theta}\big[\cos\theta \cos(t\sin\theta) - \sin\theta\sin(t\sin\theta)\big]\,d\theta \\ & = & \displaystyle \int_0^{2\pi} \frac{\partial}{\partial \theta}\big[e^{t\cos\theta} \sin(t\sin\theta)\big]\,d\theta \\ & = & \Big[ e^{t\cos\theta}\sin(t\sin\theta)\Big]_0^{2\pi} \; = \; 0 \end{array}$ Since $f(0) = 2\pi$ , the desired integral is $f(1) = \boxed{2\pi}$ .

Alternatively, complex analysis, using the substitution $z = e^{i\theta}$ , tells us that $\int_0^{2\pi} e^{\cos\theta} e^{i\sin\theta}\,d\theta \; =\; \frac{1}{i}\int_{|z|=1} \frac{e^z}{z}\,dz \; =\; 2\pi \mathrm{Res}_{z=0} \frac{e^z}{z} = 2\pi$ and we obtain the integral of the question by taking real parts. This approach also tells us that $\int_0^{2\pi} e^{\cos\theta} \sin(\sin\theta)\,d\theta \; = \; 0 \;,$ considering imaginary parts.

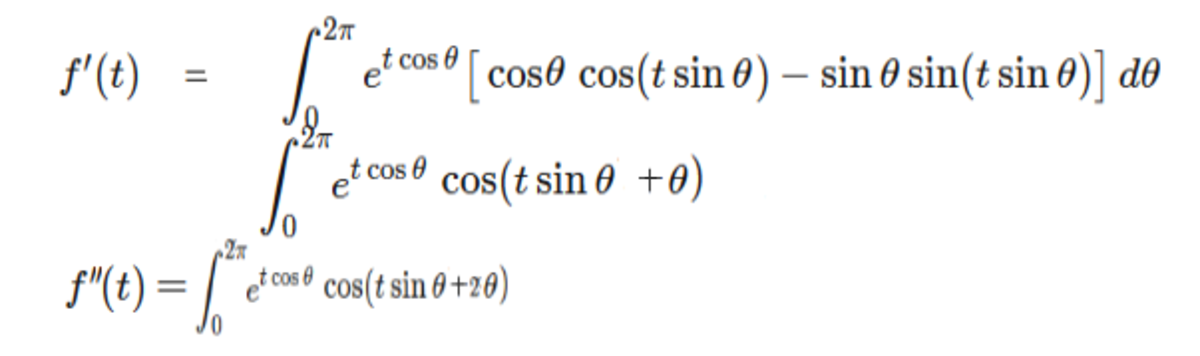[ Similarly, the nth derivitive will be fn(t)= exp(tcos(theta)(cos(tsin(theta)+ntheta))

fn(0)=0 for all n $$ cos(ntheta) integrated from 0 to 2pi is 0

f(0)=2*pi

Since all the derivitive terms are 0 the taylor expansion of f(t) shows f is a constant function ;

Therefore f(t)=2*pi for all values of t

hence, f(1)=2*pi

in(exp(cos(x))*cos(sin(x)),x=0 to 2pi)

ans13 = 6.28318530717958 ± 1.4e-13

ans13/pi

ans14 = 2.00000000000000

=> Solution is 2 $\pi$ => Fast and good! ;-)