Trigonometry! #11

Geometry Level 4

Points D D and E E are taken on the side B C BC of Δ A B C \Delta ABC such that B D = D E = E C BD=DE=EC . If ∠ B A D = x \angle BAD = x , ∠ D A E = y \angle DAE = y , ∠ E A C = z \angle EAC = z , then the value of sin ⁡ ( x + y ) sin ⁡ ( y + z ) sin ⁡ x sin ⁡ z \frac {\sin (x+y) \sin (y+z)}{\sin x \sin z} is

This problem is part of the set Trigonometry .


The answer is 4.

Omkar Kulkarni by Omkar Kulkarni , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

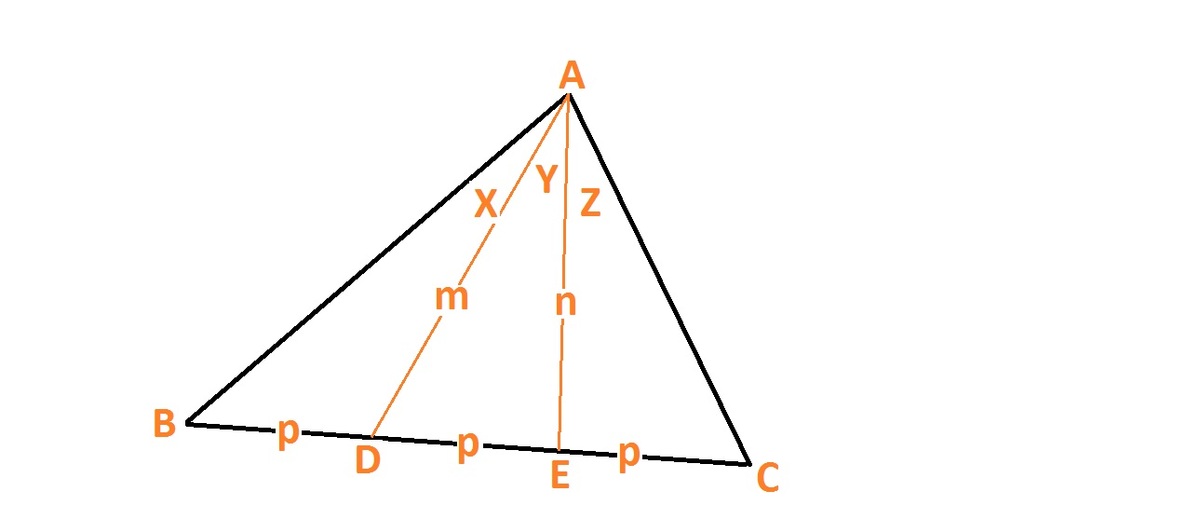L e t B D = D E = E C = p , A D = m , A E = n S i n ( x + y ) / 2 p = S i n B / n , S i n ( y + z ) / 2 p = S i n C / m S i n ( x ) / p = S i n B / m , S i n ( z ) / p = S i n C / n ∴ S i n ( x + y ) ∗ S i n ( y + z ) S i n ( x ) ∗ S i n ( z ) = 2 p ∗ S i n B / n ∗ 2 p ∗ S i n C / m p ∗ S i n B / m ∗ p ∗ S i n C / n = 4 Let~ BD=DE=EC=p, ~~AD=m, AE=n\\ Sin(x+y)/2p=SinB/n,~~Sin(y+z)/2p =SinC/m\\ Sin(x)/p=SinB/m,~~Sin(z)/p=SinC/n\\\therefore~\dfrac{Sin(x+y)*Sin(y+z) } { Sin(x)*Sin(z)}\\ =\dfrac{2p*SinB/n *2p*SinC/m}{p*SinB/m *p*SinC/n}\\=\boxed{\huge{4} }

6 Helpful 0 Interesting 0 Brilliant 0 Confused
Ayush Garg
Mar 3, 2015

The most obvious way would be to use sine rule.. However I have another way .... Sin(x+y) can be written as 2 x (area of triangle ABE) / (AB X AE).

Substituting for all 4 ratios. The answer is then quite easy to get

4 Helpful 0 Interesting 0 Brilliant 0 Confused

You see the expression for area of triangle is eventually derived from sine rule. Nonetheless great creativity.

Prayas Rautray - 3 years, 9 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...