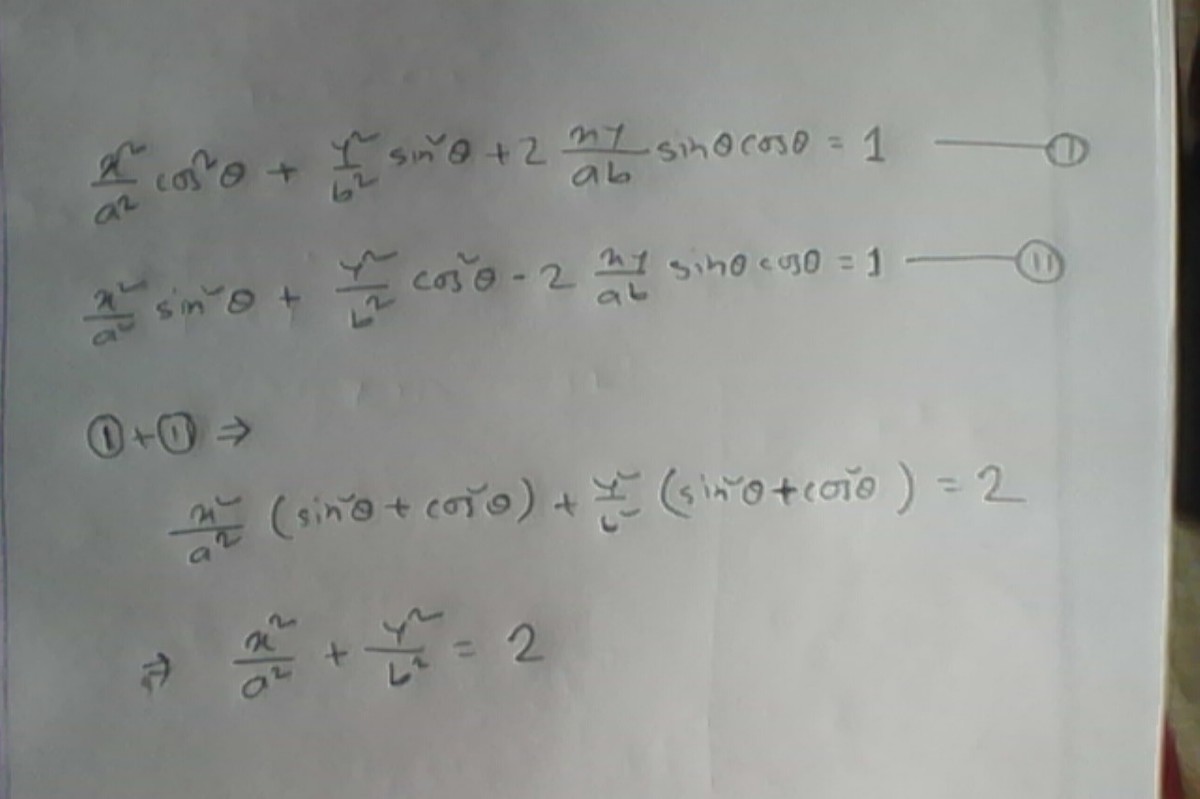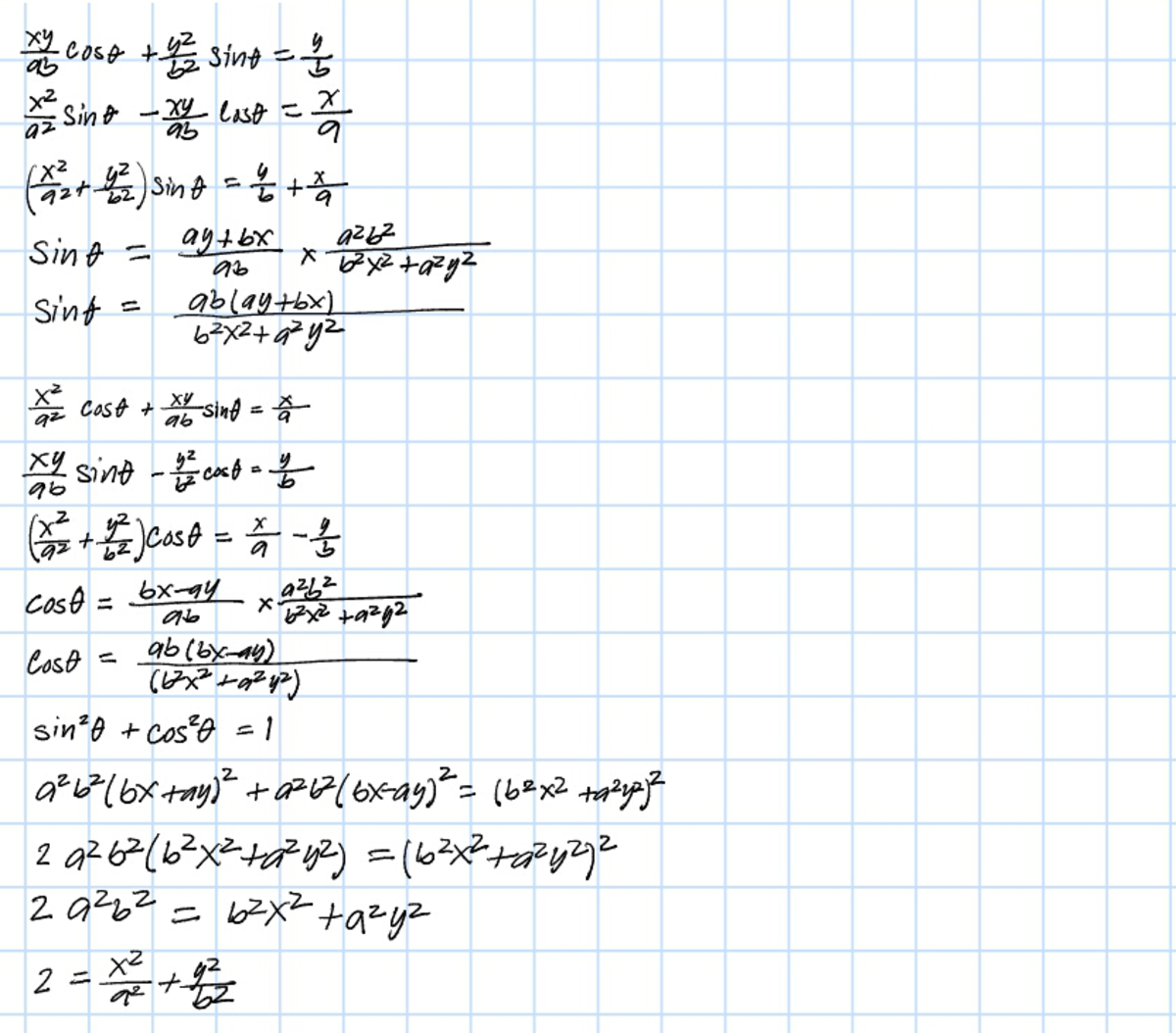Trigonometry! #101

Geometry Level 2

If x a cos ⁡ θ + y b sin ⁡ θ = 1 \frac{x}{a}\cos\theta+\frac{y}{b}\sin\theta=1 x a sin ⁡ θ − y b cos ⁡ θ = 1 \frac{x}{a}\sin\theta-\frac{y}{b}\cos\theta=1 then which of the following holds true?

This problem is part of the set Trigonometry .

x 2 a 2 + y 2 b 2 = 2 \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=2 x 2 + y 2 = a 2 + b 2 x^{2}+y^{2}=a^{2}+b^{2} x 2 − y 2 = a 2 − b 2 x^{2}-y^{2}=a^{2}-b^{2} a 2 x 2 + b 2 y 2 = 1 a^{2}x^{2}+b^{2}y^{2}=1

Omkar Kulkarni by Omkar Kulkarni , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Anwar Arif
Feb 12, 2015

2 Helpful 0 Interesting 0 Brilliant 0 Confused
James Wilson
Dec 19, 2020

Assuming the variables are all real numbers, start by multiplying the second equation by i i and then adding the equations. x a cos ⁡ θ + y b sin ⁡ θ + i ( x a sin ⁡ θ − y b cos ⁡ θ ) = 1 + i \frac{x}{a}\cos{\theta}+\frac{y}{b}\sin{\theta} + i\Big(\frac{x}{a}\sin{\theta}-\frac{y}{b}\cos{\theta}\Big)=1+i ( x a − i y b ) ( cos ⁡ θ + i sin ⁡ θ ) = 1 + i \Big(\frac{x}{a}-i\frac{y}{b}\Big)(\cos{\theta}+i\sin{\theta})=1+i Take the modulus squared on both sides of the equation: ∣ ( x a − i y b ) ( cos ⁡ θ + i sin ⁡ θ ) ∣ 2 = ∣ 1 + i ∣ 2 \Big|\Big(\frac{x}{a}-i\frac{y}{b}\Big)(\cos{\theta}+i\sin{\theta})\Big|^2=|1+i|^2 ∣ x a − i y b ∣ 2 ∣ cos ⁡ θ + i sin ⁡ θ ∣ 2 = 2 \Big|\frac{x}{a}-i\frac{y}{b}\Big|^2|\cos{\theta}+i\sin{\theta}|^2=2 ( x 2 a 2 + y 2 b 2 ) ( 1 ) = 2 \Big(\frac{x^2}{a^2}+\frac{y^2}{b^2}\Big)(1) = 2

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Roman Frago
Feb 10, 2015

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...