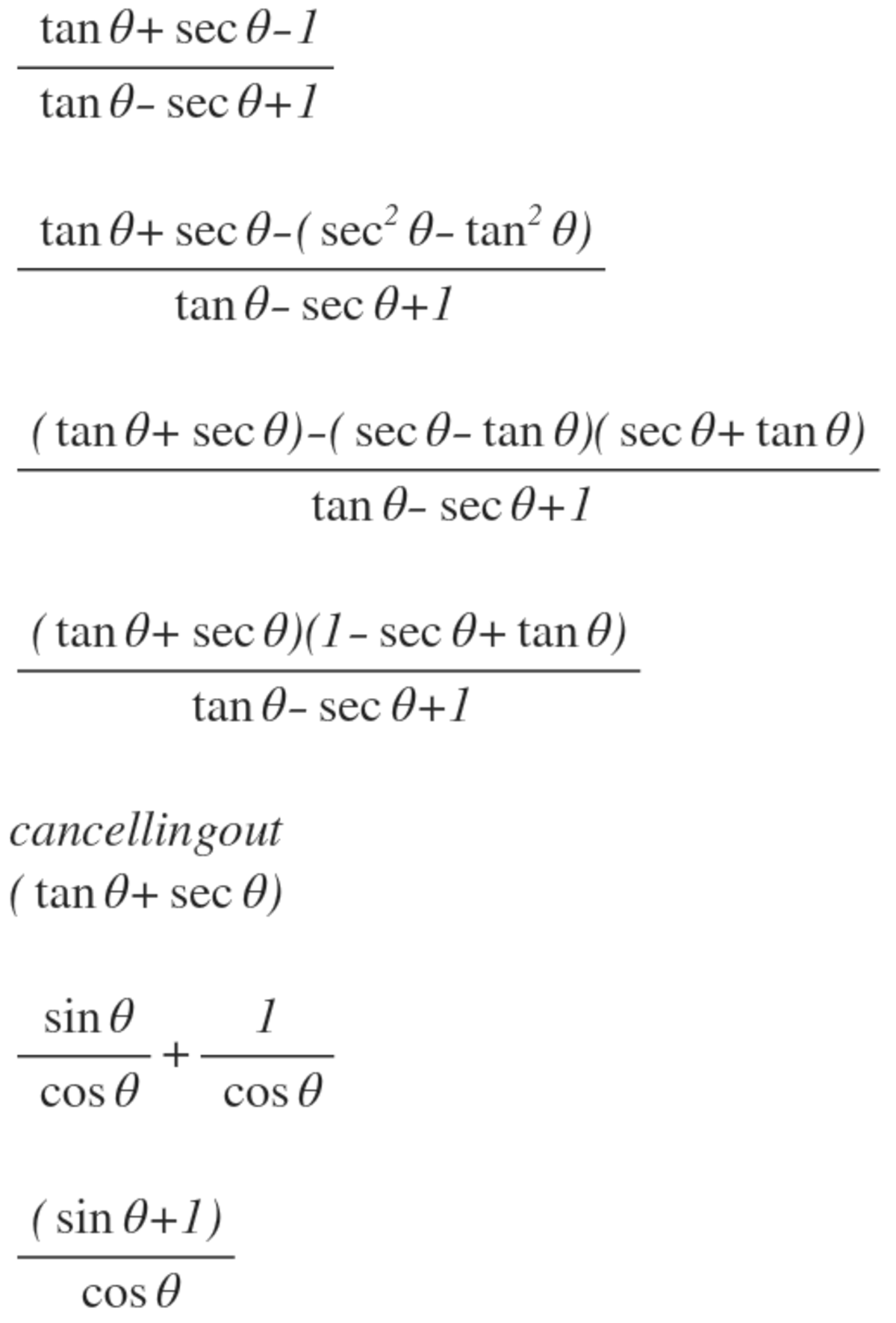Half Angle Formula Required?

Geometry Level 3

For θ ∈ ( 0 , π 2 ) \theta\in\left(0,\frac{\pi}{2}\right) , which of the following is equivalent to the expression given below? tan ⁡ θ + sec ⁡ θ − 1 tan ⁡ θ − sec ⁡ θ + 1 \frac{\tan\theta+\sec\theta-1}{\tan\theta-\sec\theta+1}

This problem is part of the set Trigonometry .

1 − sin ⁡ θ cos ⁡ θ \frac{1-\sin\theta}{\cos\theta} 1 + cos ⁡ θ sin ⁡ θ \frac{1+\cos\theta}{\sin\theta} 1 + sin ⁡ θ cos ⁡ θ \frac{1+\sin\theta}{\cos\theta} cos ⁡ θ 1 + sin ⁡ θ \frac{\cos\theta}{1+\sin\theta}

View wiki
Omkar Kulkarni by Omkar Kulkarni , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

5 solutions

Roman Frago
Feb 10, 2015

12 Helpful 0 Interesting 0 Brilliant 0 Confused

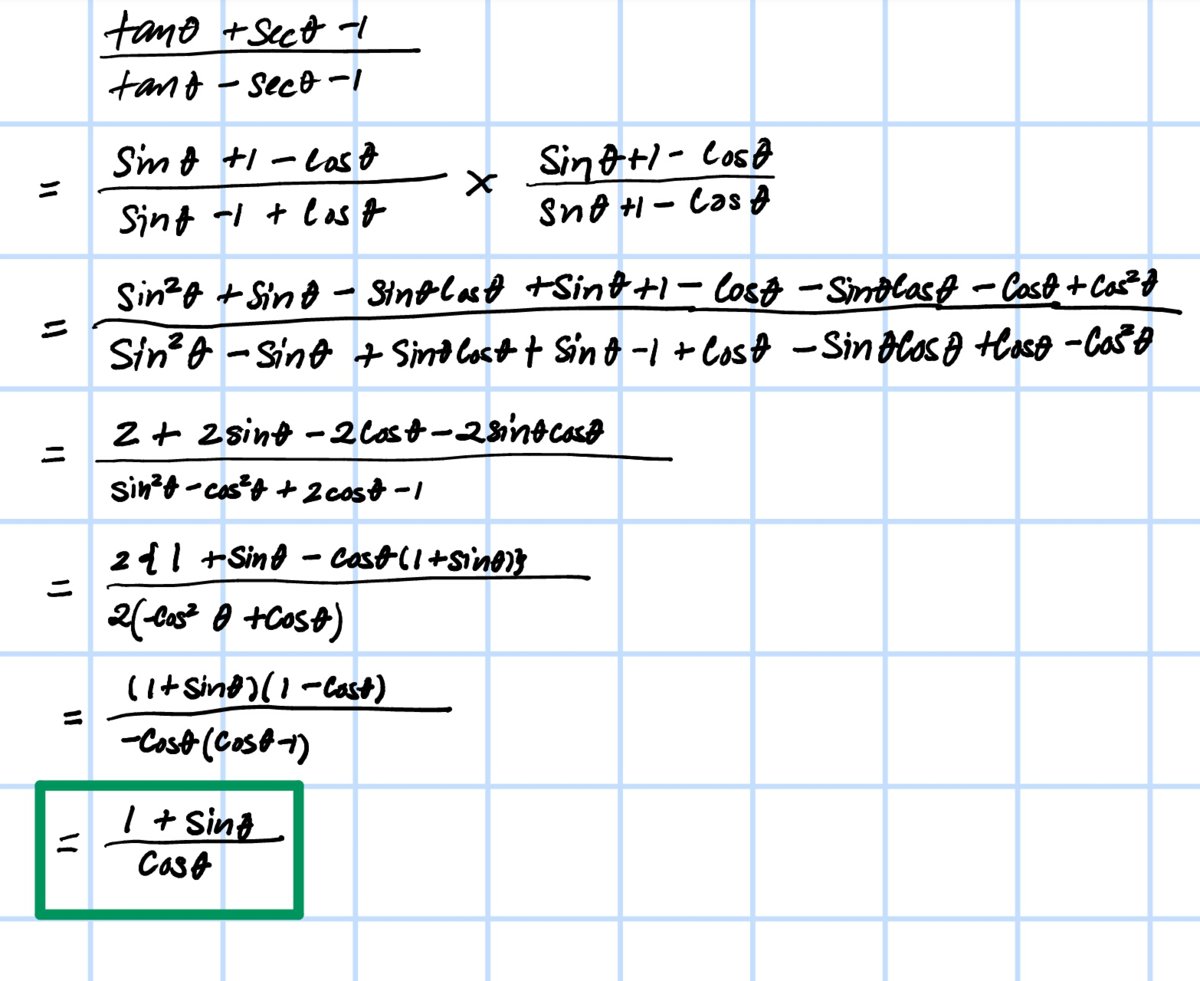
your method is same as mine

Ramez Hindi - 6 years, 4 months ago

how to get that 1st = ?

宥 神 - 6 years, 4 months ago

Multiply the numerator and denominator of the given expression by tan ⁡ ( θ ) − sec ⁡ ( θ ) − 1. \tan(\theta) - \sec(\theta) - 1. For the numerator we then have

( ( t a n ( θ ) + sec ⁡ ( θ ) ) − 1 ) ( ( tan ⁡ ( θ ) − sec ⁡ ( θ ) ) − 1 ) = ((tan(\theta) + \sec(\theta)) - 1)((\tan(\theta) - \sec(\theta)) - 1) =

tan ⁡ 2 ( θ ) − sec ⁡ 2 ( θ ) − 2 tan ⁡ ( θ ) + 1 = − 2 tan ⁡ ( θ ) \tan^{2}(\theta) - \sec^{2}(\theta) - 2\tan(\theta) + 1 = -2\tan(\theta)

since 1 + tan ⁡ 2 ( θ ) = sec ⁡ 2 ( θ ) . 1 + \tan^{2}(\theta) = \sec^{2}(\theta). For the denominator we then have

( t a n ( θ ) − sec ⁡ ( θ ) ) + 1 ) ( ( tan ⁡ ( θ ) − sec ⁡ ( θ ) ) − 1 ) = (tan(\theta) - \sec(\theta)) + 1)((\tan(\theta) - \sec(\theta)) - 1) =

tan ⁡ 2 ( θ ) + sec ⁡ 2 ( θ ) − 2 tan ⁡ ( θ ) sec ⁡ ( θ ) − 1 = \tan^{2}(\theta) + \sec^{2}(\theta) - 2\tan(\theta)\sec(\theta) - 1 =

2 tan ⁡ 2 ( θ ) − 2 tan ⁡ ( θ ) sec ⁡ ( θ ) = 2 tan ⁡ ( θ ) ( tan ⁡ ( θ ) − sec ⁡ ( θ ) ) 2\tan^{2}(\theta) - 2\tan(\theta)\sec(\theta) = 2\tan(\theta)(\tan(\theta) - \sec(\theta)) .

So the given expression is transformed to

− 2 tan ⁡ ( θ ) 2 tan ⁡ ( θ ) ( tan ⁡ ( θ ) − sec ⁡ ( θ ) ) = 1 sec ⁡ ( θ ) − tan ⁡ ( θ ) = cos ⁡ ( θ ) 1 − sin ⁡ ( θ ) = 1 + sin ⁡ ( θ ) cos ⁡ ( θ ) \dfrac{-2\tan(\theta)}{2\tan(\theta)(\tan(\theta) - \sec(\theta))} =\dfrac{1}{\sec(\theta) - \tan(\theta)} = \dfrac{\cos(\theta)}{1 - \sin(\theta)} = \dfrac{1 + \sin(\theta)}{\cos(\theta)} ,

where the last step was achieved by multiplying top and bottom by ( 1 + sin ⁡ ( θ ) ) (1 + \sin(\theta)) .

5 Helpful 0 Interesting 0 Brilliant 0 Confused

U HV done the hard way..Take theta as A --> tan A + sec A -(sec^2-tan^2)/tan A-sec A+1.....since..{1+tan^2=sec^2}.

--> tanA + secA -(secA+tanA)(secA-tanA)/tan A-sec A+1

--> (tanA+secA)(1-secA+tanA)/tan A-sec A+1

cut the common brackets out..

we are left with

=tanA+secA

=sinA/cosA + 1/cosA

sinA+1/cosA

Arnab Sinha - 6 years, 4 months ago

Log in to reply

Yes I also did your way , but selected the answer as mirror image of it.

U Z - 6 years, 4 months ago

Easiest way.. I did it same way..

Bhupendra Jangir - 6 years, 2 months ago
Aaaaa Bbbbb
Feb 11, 2015

s i n ( θ ) + 1 − c o s ( θ ) s i n ( θ ) − 1 + c o s ( θ ) \frac{sin(\theta)+1-cos(\theta)}{sin(\theta)-1+cos(\theta)} = 2 s i n ( θ 2 ) c o s ( θ 2 ) + 1 − 1 + 2 s i n 2 ( θ 2 ) 2 s i n ( θ 2 ) c o s ( θ 2 ) − 1 + 1 − 2 s i n 2 ( θ 2 ) =\frac{2sin(\frac{\theta}{2})cos(\frac{\theta}{2})+1-1+2sin^{2}(\frac{\theta}{2})}{2sin(\frac{\theta}{2})cos(\frac{\theta}{2})-1+1-2sin^{2}(\frac{\theta}{2})} = s i n ( θ 2 ) c o s ( θ 2 ) + s i n 2 ( θ 2 ) s i n ( θ 2 ) c o s ( θ 2 ) − s i n 2 ( θ 2 ) =\frac{sin(\frac{\theta}{2})cos(\frac{\theta}{2})+sin^{2}(\frac{\theta}{2})}{sin(\frac{\theta}{2})cos(\frac{\theta}{2})-sin^{2}(\frac{\theta}{2})} = c o s ( θ 2 ) + s i n ( θ 2 ) c o s ( θ 2 ) − s i n ( θ 2 ) =\frac{cos(\frac{\theta}{2})+sin(\frac{\theta}{2})}{cos(\frac{\theta}{2})-sin(\frac{\theta}{2})} = 1 + s i n ( θ ) c o s ( θ ) =\boxed{\frac{1+sin(\theta)}{cos(\theta)}}

4 Helpful 0 Interesting 0 Brilliant 0 Confused

how did you achieve the last step

John Doe - 6 years, 3 months ago

Log in to reply

It can be by multiplying numerator and denominator with its numerator ...

aaaaaa bbbbbb - 6 years, 3 months ago
Afreen Sheikh
Apr 14, 2015

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Ramez Hindi
Feb 10, 2015

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...