Trigonometry! #121

Geometry Level 2

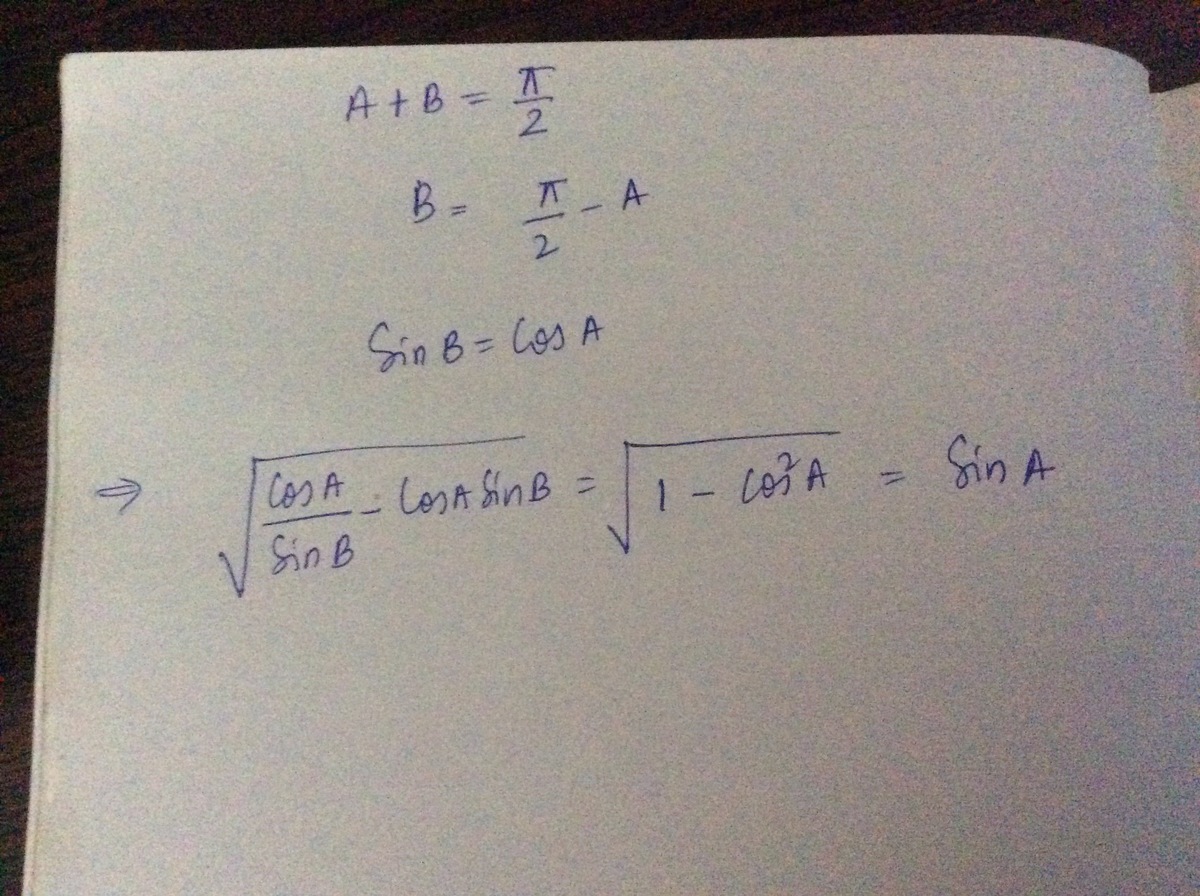
Given that A A and B B are complementary acute angles, then

cos ⁡ A sin ⁡ B − cos ⁡ A sin ⁡ B = ? \sqrt{\frac{\cos A}{\sin B}-\cos A \sin B} = \, \color{#D61F06}{?}

Assume A A and B B are positive.

cos ⁡ A \cos A sin ⁡ A \sin A tan ⁡ A \sqrt{\tan A} tan ⁡ A \tan A

Omkar Kulkarni by Omkar Kulkarni , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

3 Helpful 0 Interesting 0 Brilliant 0 Confused
Eli Ross Staff
May 16, 2016

Relevant wiki: Trigonometric Co-function Identities

Note that sin ⁡ B = sin ⁡ ( 9 0 ∘ − A ) = cos ⁡ ( A ) , \sin B = \sin(90^\circ - A) = \cos(A), so the expression becomes cos ⁡ A cos ⁡ A − cos ⁡ A cos ⁡ A = 1 − cos ⁡ 2 A = sin ⁡ 2 A = ∣ sin ⁡ A ∣ = sin ⁡ A , \sqrt{\frac{\cos A}{\cos A} - \cos A \cos A} = \sqrt{1-\cos^2A} = \sqrt{\sin^2 A} = \left|\sin A\right| =\sin A, where we have made use of the fact that sin ⁡ A > 0 \sin A > 0 and the pythagorean identity sin ⁡ 2 A + cos ⁡ 2 A = 1. \sin^2 A + \cos^2 A = 1.

3 Helpful 0 Interesting 1 Brilliant 1 Confused

Is this expression really equivalent to the sine? Shouldn't a restricted domain be stated? (i.e., 0 + 2 π n ≤ x ≤ π + 2 π n 0+2\pi n \leq x \leq \pi+2\pi n )

Edwin Hughes - 5 years ago

Why it can't be sin A

Rohit Pati - 2 years, 4 months ago
Mevlut Esen
May 18, 2016

An accute angle means an angle that accumulate 90 degrees toplam your angle. From that; cosA/sinB=1 and cosA×sinB=cos^2 (A) We all know 1-cos^2 (A)=sin^2 (A)

Now from here sqrt (sin^2 (A))=sinA

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...