Trigonometry! #17

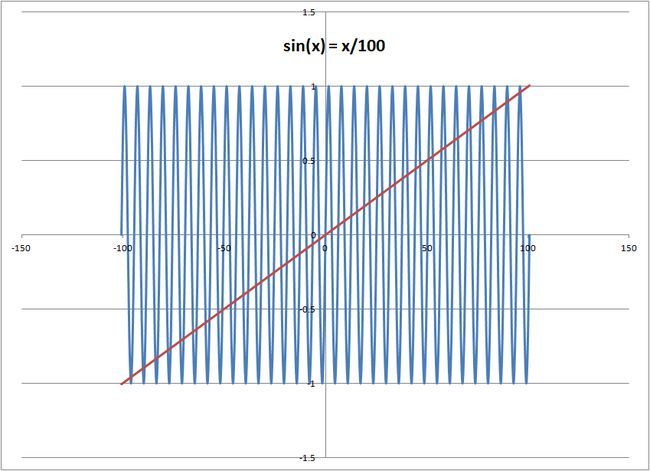
$100y=x$ and $y=\sin(x) \rightarrow \sin(x)=\frac{x}{100}$

As $-1≤\sin(x)≤1$ , $-100≤100\sin(x)≤100 \Rightarrow -100≤x≤100$ .

Now, the period of sine is $2\pi$ . So the number of waves we will consider will be $\frac{200}{2\pi} \approx 31.8$ , which we will consider as $32$ .

The line will intersect each curve twice, and hence we would have $64$ intersections. But the intersection at $(0,0)$ is common to both waves.

Therefore the answer, $\boxed{63}$ .

$-1\leq \sin x\leq 1 \Rightarrow -1\leq \frac{x}{100}\leq 1 \Rightarrow -100\leq x\leq 100$ $100/{2\pi} \approx 15.9155$ For each period $\frac{x}{100}$ touches to $\sin x$ two times. But $0$ are counted two times so real roots are $16\times 4-1=\boxed{63}$

Image credits: @Chew-Seong Cheong