Trigonometry

Geometry Level 2

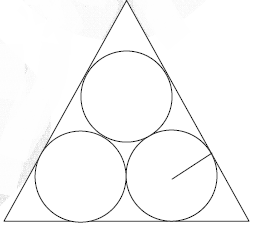
In an equilateral triangle, 3 coins of radii 1 unit each are kept so that they touch each other and also the sides of the triangle.

The area of the triangle is :

6 + 4 3 6 + 4\sqrt 3 12 + 7 3 12 + 7\sqrt 3 3 + 4 3 3 + 4\sqrt 3 4 + 2 3 4 + 2\sqrt 3

Hardik Siloiya by Hardik Siloiya , 19, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Hardik Siloiya
Jan 27, 2016

The line joining the vertex of the triangle and the centre of the coin makes angle π/6 with the sides of the triangle. The length of each of the sides of the equilateral triangle is 2 + 2 cot π/6 =2(1 + √ .3 ). 

       Hence its area is  √ .3/4(1+√ .3 )^2  = 6+ 4√ .3
4 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...