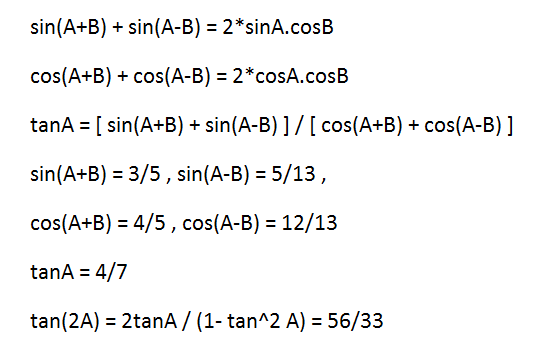Trigonometry

$\begin{aligned} \cos (A+B) & = \frac{4}{5} \quad \quad \small \color{#3D99F6}{\text{Given}} \\ \implies \tan (A+B) & = \frac{3}{4} \\ \frac{\tan A + \tan B}{1-\tan A \tan B} & = \frac{3}{4} \\ 4\tan A + 4 \tan B & = 3 - 3\tan A \tan B \\ \implies \tan B & = \frac{3-4\tan A}{4+3\tan A} \end{aligned}$

---

$\begin{aligned} \sin (A-B) & = \frac{5}{13} \quad \quad \small \color{#3D99F6}{\text{Given}} \\ \implies \tan (A-B) & = \frac{5}{12} \\ \frac{\tan A - \tan B}{1+\tan A \tan B} & = \frac{5}{12} \\ 12\tan A - 12\tan B & = 5 + 5\tan A \tan B \\ \implies \tan B & = \frac{12\tan A -5}{12+5\tan A} \end{aligned}$

---

$\begin{aligned} \implies \frac{3-4\tan A}{4+3\tan A} & = \frac{12\tan A -5}{12+5\tan A} \\ (3-4\tan A)(12+5\tan A) & = (12\tan A -5)(4+3\tan A) \\ 36-33\tan A - 20 \tan^2 A & = 36 \tan^2 A + 33 \tan A -20 \\ 56 \tan^2 A + 66 \tan A - 56 & = 0 \\ 28 \tan^2 A + 33 \tan A - 28 & = 0 \\ (7\tan A -4)(4\tan A + 7) & = 0 \\ \implies \tan A & = \frac{4}{7} \quad \quad \small \color{#3D99F6}{\text{Since } 0^\circ < A < 45^\circ} \end{aligned}$

---

$\begin{aligned} \implies \tan 2A & = \frac{\frac{8}{7}}{1-\frac{16}{49}} = \boxed{\dfrac{56}{33}} \end{aligned}$

$\cos(A+B) = \dfrac{4}{5} \implies A+B = \cos^{-1} \left( \dfrac{4}{5} \right)$ ......(1)

$\sin(A-B) = \dfrac{5}{13} \implies A-B = \sin^{-1} \left( \dfrac{5}{13} \right)$ ......(2)

(1) + (2) $\implies 2A = \cos^{-1} \left( \dfrac{4}{5} \right) + \sin^{-1} \left( \dfrac{5}{13} \right)$

Therefore,

$\tan 2A = \tan \left( \cos^{-1} \left( \dfrac{4}{5} \right) + \sin^{-1} \left( \dfrac{5}{13} \right) \right)\\ =\dfrac{\tan \left( \cos^{-1} \left( \dfrac{4}{5} \right) \right) + \tan \left( \sin^{-1} \left( \dfrac{5}{13} \right) \right)}{1 - \tan \left( \cos^{-1} \left( \dfrac{4}{5} \right) \right) \tan \left( \sin^{-1} \left( \dfrac{5}{13} \right) \right)}\\ =\dfrac{\dfrac{3}{4} + \dfrac{5}{12}}{1 - \left( \dfrac{3}{4} \right) \left( \dfrac{5}{12} \right)}\\ =\dfrac{ \dfrac{7}{6}}{1 - \dfrac{15}{48}} = \boxed{\dfrac{56}{33}}$

OR

$\cos(A+B) = \dfrac{4}{5} \implies \tan(A+B) = \dfrac{3}{4}\\ \sin(A-B) = \dfrac{5}{13} \implies \tan(A-B) = \dfrac{5}{12}$

$\tan 2A\\ = \tan((A+B) + (A-B))\\ =\dfrac{\tan(A+B) + \tan(A-B)}{1 - \tan(A+B)\tan(A-B)}\\ =\dfrac{\dfrac{3}{4} + \dfrac{5}{12}}{1 - \left( \dfrac{3}{4} \right) \left( \dfrac{5}{12} \right)}\\ =\dfrac{ \dfrac{7}{6}}{1 - \dfrac{15}{48}} = \boxed{\dfrac{56}{33}}$

Here is a geometric way to solve the problem:

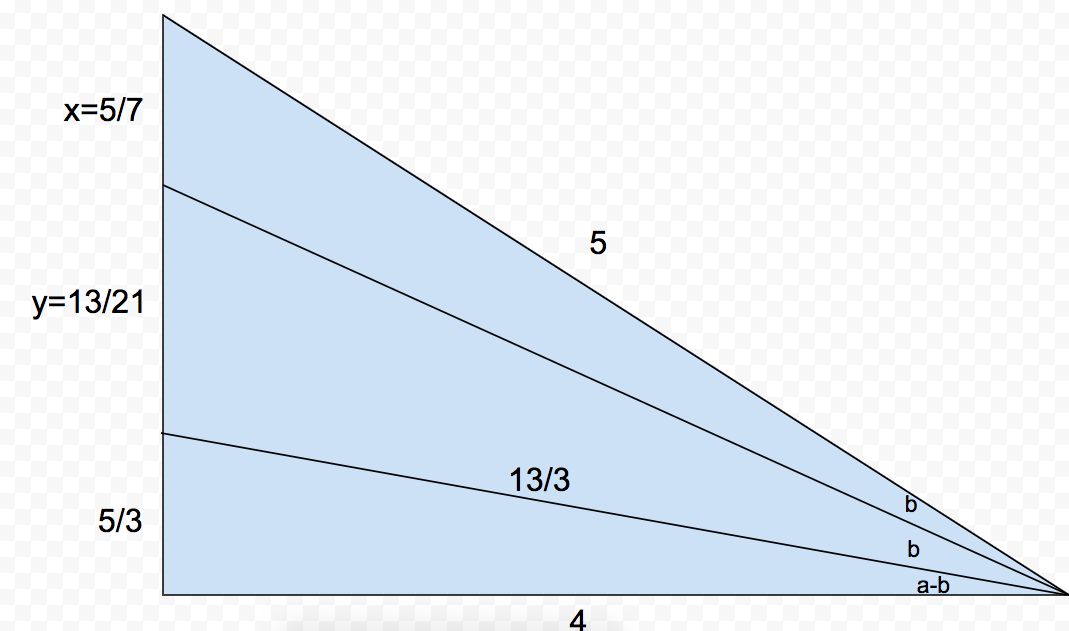
Here, the values of $(x)$ and $(y)$ are derived from a system of equations with the angle bisector theorem and the fact that $(x+y+1.6667) = 3$ by the Pythagorean theorem. The values $(\frac{13}{3}$ )) and $(\frac{5}{3}$ )) are derived from the fact that the Triangle with those lengths is a $5-12-13$ triangle dilated with a factor of $0.333$ since $12*0.333=4$ , and $12$ is derived from a $5-12-13$ triangle as $sin(a-b) = (\frac{5}{13}$ )).

Next, using $tan(A) = (\frac{4}{7}$ )), then $tan(2A)$ can be evaluated using substitution and the tan double angle formula.

Applying product-to-sum identities, we have thee following:

$\cos(A + B)\cos(A - B) = \frac{48}{65}, (1a)$

$\sin(A + B)\sin(A - B) = \frac{15}{65}, (1b)$

$\sin(A + B)\cos(A - B) = \frac{36}{65}, (2a)$

$\cos(A + B)\sin(A - B) = \frac{20}{65}. (2b)$

Subtract $(1a)$ and $(1b)$ , and add $(2a)$ and $(2b)$ respectively yields

$\cos(A + B)\cos(A - B) - \sin(A + B)\sin(A - B) = \frac{33}{65} = \cos(2A), (3)$

$\sin(A + B)\cos(A - B) + \cos(A + B)\sin(A - B) = \frac{56}{65} = \sin(2A). (4)$

Divide $(4)$ and $(3)$ gives

$\tan(2A) = \frac{\sin(2A)}{\cos(2A)} = \boxed{\frac{56}{33}}.$

Note : $\cos(A - B) = \frac{12}{13}$ and $\sin(A + B) = \frac{3}{5}$ .

Sin(A+B. + A - B) = sin (2A) Sin(A + B + A- B) = Sin(A+B)cos(A-B) + cos(A+B)sin(A-B) cos(A + B) = 4/5 so sin(A + B) = 3/5 sin(A-B) = 5/13 so cos(A-B) = 12/13 sin(2A) = 3/5 × 12/13 + 4/5 × 5/13 = 56/65 So cos(2A) = 33/65 Therefore tan(2A) =56/65 ÷ 33/65 = 56/33

Easy ... Like whi dont know that..this is old school . dont even need to calculateur that you can JUST do a quick resolution in your head

Inverse sin(5/13) = 22.62 degrees = A - B

Inverse cos(4/5) = 36.87 degrees = A + B

Adding two equations yields: 59.49 degrees = 2 *A

Tan(59.49) = 1.697 = 56/33