Trigonometry! #10
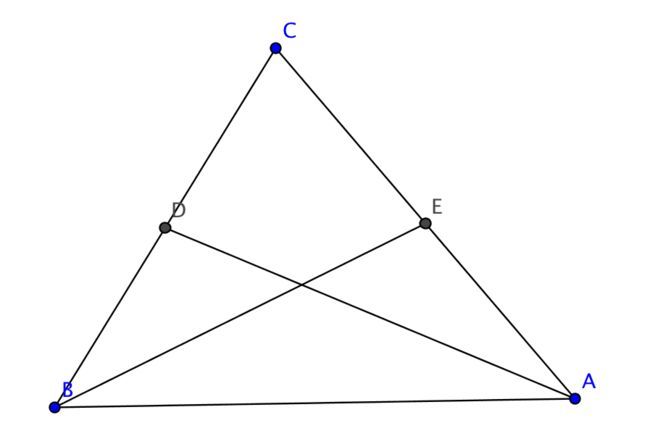
Points D and E are the midpoints of sides B C and C A , respectively, of △ A B C .
If A D = 5 and B C = B E = 4 , then find the length of C A .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions

Let ∠ E B C = θ
In Δ B G D , using cosine rule, we get cos θ = 3 2 2 5
In Δ E B C , using cosine rule, we get E C = 7
∴ A C = 2 7
We can either use Apollonius theorem.
For this question (figure):-
A B 2 + A C 2 = 2 ( A D 2 + B D 2 )
A B 2 + B C 2 = 2 ( B E 2 + ( 2 A C ) 2 )
Substituting the values and equating the 2 equations, we get:
2 3 A C 2 = 4 2
A C 2 = 2 8
A C = 2 7
Thus, the answer is: A C = 2 7
Using cosine formula 2 times.
AE = EC = x Angle BCA= a
In triangle BCE: 16= 16+ x^2 -8x cos a X= 8. Cos a
In triangle ADC 25= 4x^2 + 4 -8x cos a 25=4x^2 + 4 - x^2 21=3x^2 X^2 = 7 hence, x= sqrt 7,
AC= 2x= 2.sqrt7
Same as Omkar Kulkarni but putting little detail.
Let G be the centroid, intersection of AD and BE.
I
n
△
D
B
G
,
C
o
s
D
B
G
=
2
∗
2
∗
8
/
3
(
D
B
)
2
+
(
2
/
3
∗
B
E
)
2
−
(
A
D
/
3
)
2
=
2
∗
2
∗
8
/
3
2
2
+
(
8
/
3
)
2
−
(
5
/
3
)
2
=
3
2
2
5
.
I
n
△
C
B
E
C
o
s
C
B
E
=
C
o
s
D
B
G
=
2
∗
4
∗
4
4
2
+
4
2
−
C
E
2
=
3
2
3
2
−
C
E
2
.
∴
C
E
=
7
.
S
o
A
C
=
2
7
.
How did you get value (8/3) and (5/3)?
Log in to reply
I have added an expression on line three. Please feel free to ask if still there is any doubt.
We can solve it using geometry also. Applying Apollonius thm to triangle ABC twice.Once considering AD as a median and nxt BE as a median.
Extreme shortcut: given that AD = 5 and BC = 4, CA must be close to AD. The only value close to 5 amongst the available choices is 2 \sqrt {7}.
Use formula for length of median drawn to a side in terms of lengths of sides.it can be referred in chapter solution of triangles. Apply that to BE & AD to get two equations in AB & AC . Solve them to get the answer as 2sq.root7..
Let, C E = E A = y . Using cosine rule, 4 2 = 4 2 + y 2 − 2 ( 4 ) ( y ) . cos C and, 4 2 = 4 2 + y 2 − 8 y . cos C . We observe that, y 2 − 8 y . cos C = 0 . ⋯ ( 1 ) Again, 5 2 = ( 2 y ) 2 + 2 2 − 2 ( 2 ) ( 2 y ) . cos C . 5 2 = 4 y 2 + 2 2 − 8 y . cos C . This can be written as, 5 2 = 3 y 2 + 2 2 + y 2 − 8 y . cos C . ⋯ ( 2 ) Substituting equation (1) in (2) we get, 2 5 = 3 y 2 + 4 3 y 2 = 2 1 y 2 = 7 y = 7 We had assumed that C E = E A = y .
The question is to find the value of C A , which is C E + E A .
C A = y + y
C A = 2 7