#Trigonometry-3
The value of cot θ cot 2 θ − cot 2 θ cot 3 θ − cot 3 θ cot θ is:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is how to multiple guess the answer from given options. It does not solve the problem.
Log in to reply
You are right Sir. But still i thought i could post the way i used to find the result.
Log in to reply
The limitations of the software are partly to blame for the fact that we can't always make the problems in such a fashion that shortcuts and guesses won't get people to the right answers. The number of "solvers" reported is usually much higher than the number of actual solvers. On the other hand, it gets people to where they can see the real solutions, and without a penalty. So maybe it serves a purpose, too.
Using expressions cot 2 θ = 2 cot θ cot 2 θ − 1 and cot 3 θ = cot 2 θ + cot θ cot 2 θ cot θ − 1 .
These can be easily derived from sin ( α + β ) = sin α cos β + cos α sin β and cos ( α + β ) = cos α cos β − sin α sin β
The rest is basic algebra.
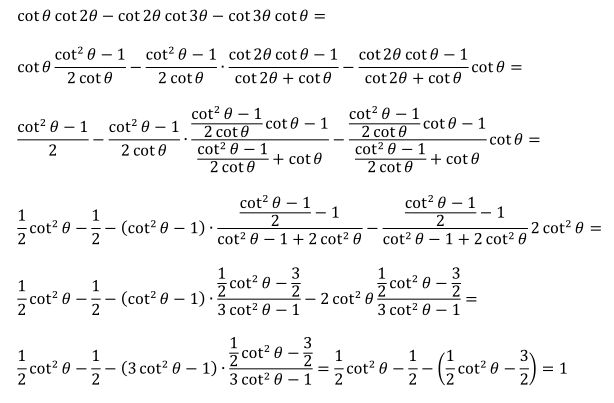
The value of the expression for θ = 6 π is 1.
But sin 6 π = 2 1 and cos 6 π = 2 3
Therefor the only option left is:
cot θ cot 2 θ − cot 2 θ cot 3 θ − cot 3 θ cot θ = 1