Trigonometry! #96
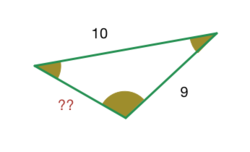 In a triangle, the lengths of the two larger sides are
1
0
and
9
respectively. If the angles are in A.P., then the length of the third side can be
In a triangle, the lengths of the two larger sides are
1
0
and
9
respectively. If the angles are in A.P., then the length of the third side can be
-
5 − 6
-
3 3
-
5
-
5 + 6
Note: Enter the sum of the serial numbers of the correct options. More than one option is correct.
This problem is part of the set Trigonometry .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
We can save steps and time by applying cosine rule on the angle which is 6 0 o .
Log in to reply
Good point. We would get
8 1 = 1 0 0 + L 2 − 1 0 ∗ L ⟹ L 2 − 1 0 ∗ L + 1 9 = 0
⟹ L = 2 1 0 ± 1 0 0 − 7 6 = 5 ± 6 .
That does save a lot of time. :)
Log in to reply
This is better
Just a little detail since it took some time for me to understand.. 8 1 = 1 0 0 + L 2 − 2 ∗ 1 0 ∗ L ∗ C o s 6 0 .
For a = 10 and b = 9 opposite to angle A and B respectively,
Cos C = (10^2 + 9^2 - c^2)/ [2(10)(9)] = (181 - c^2)/ 180
Sin A/ 10 = Sin B/ 9 = Sin C/ c {Less safe} OR
Cos A = (9^2 + c^2 - 10^2)/ [2(9)(c)] and Cos B = (10^2 + c^2 - 9^2)/ [2(10)(c)]
For C, B, A:
14.20683095, 60, 105.793169;
31.17883554, 63.72786107, 85.09330339;
29.92643487, 63.89611886, 86.17744627;
45.79316905, 60, 74.20683095.
Using sine rule, 180 d - Asin x ought to be there for obtuse A; using cosine rule, we are safe from obtuse error. Differences:
45.7931690482639, 45.7931690482640;
32.5490255281136, 21.3654423278050;
33.9696839960459, 22.2813274080656;
14.2068309517360, 14.2068309517360.
Therefore 5 - Sqrt (6) and 5 + Sqrt (6) are the two answers suitable for A.P. angles.
1 + 4 = 5
Note: In this question, I tried by substitutions rather than to solve in order.
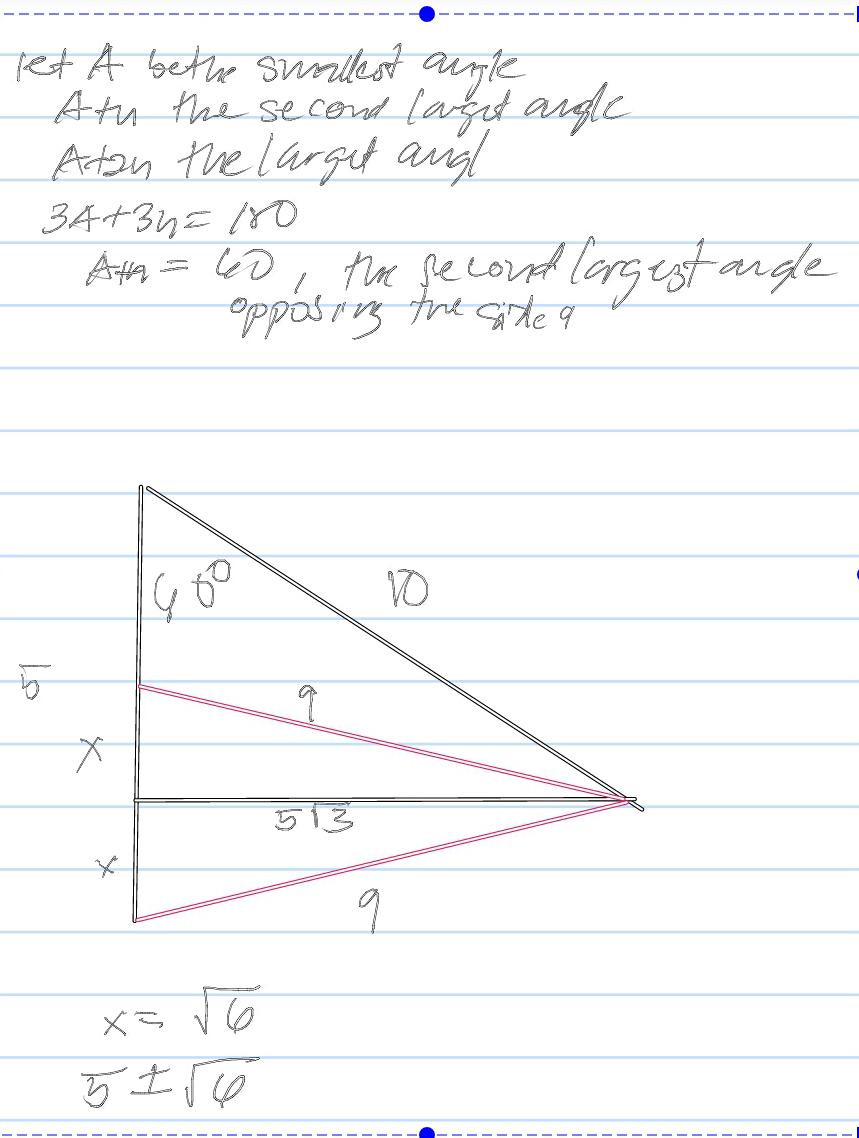
Let the angles be x − d , x and x + d for some d > 0 . Now since the three angles must sum to 1 8 0 ∘ , we know that x = 6 0 ∘ . The other two angles then sum to 1 2 0 ∘ , so for ease of calculation rename the largest angle y , which makes the smallest angle 1 2 0 ∘ − y .
Now the largest angle will be opposite the side length 1 0 and the smallest angle will be opposite the shortest side. Letting this shortest side have length L , the Sine Law gives us that
L sin ( 1 2 0 ∘ − y ) = 9 sin ( 6 0 ∘ ) = 1 0 sin ( y ) .
From the second equality we have that
sin ( y ) = 9 1 0 sin ( 6 0 ∘ ) = 9 5 3 ,
and so cos ( y ) = ± 1 − sin 2 ( y ) = ± 1 − 8 1 7 5 = ± 9 6 .
From the first equality we have that
L = sin ( 6 0 ∘ ) 9 sin ( 1 2 0 ∘ − y ) = 6 3 ( sin ( 1 2 0 ∘ ) cos ( y ) − cos ( 1 2 0 ∘ ) sin ( y ) ) =
6 3 ( 2 3 ∗ ( ± ( 9 6 ) ) + 2 1 ∗ 9 5 3 ) = ± 6 + 5 .
Thus the two possible lengths of the third side are 5 − 6 and 5 + 6 , the serial numbers of which are 1 and 4, respectively.
Thus the desired sum is 1 + 4 = 5 .