Trigonometry and Polynomials?

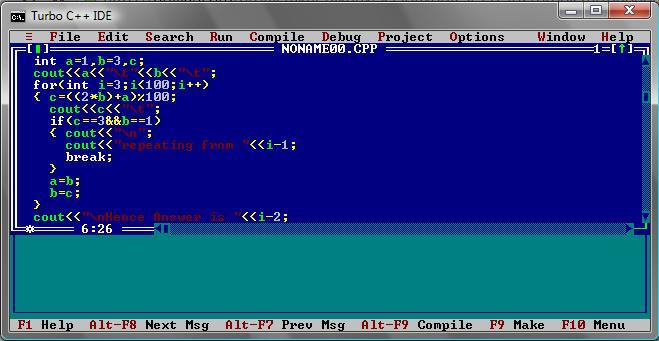
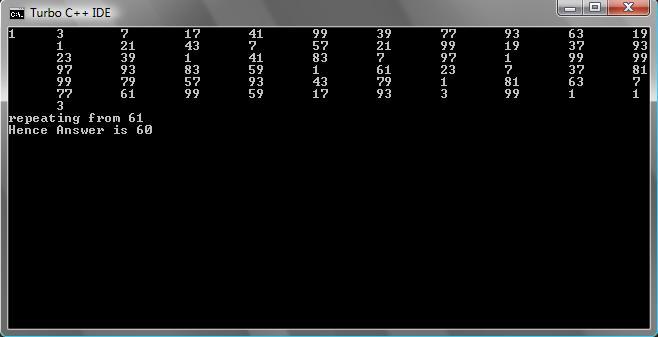
A year later I check back to this question, and realised what a complete idiot I was. THIS ISN'T A SOLUTION!!!

I won't go into the details (its very tedious) but after lots of hard work you can finally derive this:

$S(n)=\frac { { \left( 1-\sqrt { 2 } \right) }^{ n }+{ \left( 1+\sqrt { 2 } \right) }^{ n } }{ 2 }$

Since I am pretty bad at modulus, I went ahead and bashed with a computer program and got the following list from $n=0$ to $n=288$ (I manually bashed the first 26 but it was too slow):

1, 3, 7, 17, 41, 99, 239, 577, 1393, 3363, 8119, 19601, 47321, 114243, 275807, 665857, 1607521, 3880899, 9369319, 22619537, 54608393, 131836323, 318281039, 768398401, 1855077841, 4478554083, 10812186007, 26102926097, 63018038201, 152139002499, 367296043199, 886731088897, 2140758220993, 5168247530883, 12477253282759, 30122754096401, 72722761475561, 175568277047523, 423859315570607, 1023286908188737, 2470433131948081, 5964153172084899, 14398739476117879, 34761632124320657, 83922003724759193, 202605639573839043, 489133282872437279, 1180872205318713601, 2850877693509864481, 6882627592338442563, 16616132878186749607, 40114893348711941777, 96845919575610633161, 233806732499933208099, 564459384575477049359, 1362725501650887306817, 3289910387877251662993, 7942546277405390632803, 19175002942688032928599, 46292552162781456490001, 111760107268250945908601, 269812766699283348307203, 651385640666817642523007, 1572584048032918633353217, 3796553736732654909229441, 9165691521498228451812099, 22127936779729111812853639, 53421565080956452077519377, 128971066941642015967892393, 311363698964240484013304163, 751698464870122983994500719, 1814760628704486452002305601, 4381219722279095887999111921, 10577200073262678228000529443, 25535619868804452344000170807, 61648439810871582916000871057, 148832499490547618176001912921, 359313438791966819268004696899, 867459377074481256712011306719, 2094232192940929332692027310337, 5055923762956339922096065927393, 12206079718853609176884159165123, 29468083200663558275864384257639, 71142246120180725728612927680401, 171752575441025009733090239618441, 414647397002230745194793406917283, 1001047369445486500122677053453007, 2416742135893203745440147513823297, 5834531641231893991002972081099601, 14085805418356991727446091676022499, 34006142477945877445895155433144599, 82098090374248746619236402542311697, 198202323226443370684367960517767993, 478502736827135487987972323577847683, 1155207796880714346660312607673463359, 2788918330588564181308597538924774401, 6733044458057842709277507685523012161, 16255007246704249599863612909970798723, 39243058951466341909004733505464609607, 94741125149636933417873079920900017937, 228725309250740208744750893347264645481, 552191743651117350907374866615429308899, 1333108796552974910559500626578123263279, 3218409336757067172026376119771675835457, 7769927470067109254612252866121474934193, 18758264276891285681250881852014625703843, 45286456023849680617114016570150726341879, 109331176324590646915478914992316078387601, 263948808673030974448071846554782883117081, 637228793670652595811622608101881844621763, 1538406396014336166071317062758546572360607, 3714041585699324927954256733618974989342977, 8966489567412986021979830529996496551046561, 21647020720525296971913917793611968091436099, 52260531008463579965807666117220432733918759, 126168082737452456903529250028052833559273617, 304596696483368493772866166173326099852465993, 735361475704189444449261582374705033264205603, 1775319647891747382671389330922736166380877199, 4286000771487684209792040244220177366025960001, 10347321190867115802255469819363090898432797201, 24980643153221915814302979882946359162891554403, 60308607497310947430861429585255809224215906007, 145597858147843810676025839053457977611323366417, 351504323792998568782913107692171764446862638841, 848606505733840948241852054437801506505048644099, 2048717335260680465266617216567774777456959927039, 4946041176255201878775086487573351061418968498177, 11940799687771084222816790191714476900294896923393, 28827640551797370324408666871002304862008762344963, 69596080791365824871634123933719086624312421613319, 168019802134529020067676914738440478110633605571601, 405635685060423865006987953410600042845579632756521, 979291172255376750081652821559640563801792871084643, 2364218029571177365170293596529881170449165374925807, 5707727231397731480422240014619402904700123620936257, 13779672492366640326014773625768686979849412616798321, 33267072216131012132451787266156776864398948854532899, 80313816924628664590918348158082240708647310325864119, 193894706065388341314288483582321258281693569506261137, 468103229055405347219495315322724757272034449338386393, 1130101164176199035753279114227770772825762468183033923, 2728305557407803418726053543778266302923559385704454239, 6586712278991805873205386201784303378672881239591942401

Then I manually scan (Im also not good at coding) and found that the last $2$ digits repeat from this number ( $111760107268250945908601$ ) onwards.

So in order to find $111760107268250945908601=\frac { { \left( 1-\sqrt { 2 } \right) }^{ n }+{ \left( 1+\sqrt { 2 } \right) }^{ n } }{ 2 }$ I once again used a program to compute that $n=61$ .

Therefore, $61 - 1 = A = \boxed{\boxed{\boxed{\boxed{\boxed{60}}}}}$

This is the craziest question I solved so far... It should be level 6.

Extra:

If the question asks for modulo $10$ , the answer would be $12$ ,

for modulo $100$ , the answer would be $60$ ,

for modulo $1000$ , the answer would be $300$

Isn't it curious? Like if the modulo thing $\times 10$ , the answer would $\times 5$ . I don't have a proof for this but if anybody does, I'd like to see it.

For any integer $n$ :

${ P }_{ 2n }(y)=2\left( { { P }_{ n }(y) } \right) ^{ 2 }-1$

For odd number $n$ :

${ P }_{ n }(y)=y\left( 2\sum _{ k=0 }^{ \frac { n-1 }{ 2 } }{ { \left( -1 \right) }^{ k+1 }\left( { P }_{ n-1-2k }(y) \right) } \right)$

The polynomials are the Chebyshev polynomials, normally written $T_n(x)$ . They satisfy the recurrence relation $T_{n+1}(x) + T_{n-1}(x) \,=\, 2xT_n(x)$ (think $\cos(n+1)u + \cos(n-1)u \,=\, 2\cos u \cos nu$ ). Moreover, each polynomial $T_n(x)$ has degree $n$ and parity $(-1)^n$ . In fact $T_n(x) \; =\; \tfrac12n \sum_{m=0}^{\lfloor \frac12n\rfloor} (-1)^m\frac{(n-m-1)!}{m!(n-2m)!}(2x)^{n-2m} \;;$ the fact that the coefficients have alternating signs means that $T_n (i) = i^nS(n)$ for all $n \ge 0$ . Thus we obtain the recurrence relation $S(n+1) \; = \; 2S(n) + S(n-1) \;.$ Calculating modulo $4$ we see that $\begin{array}{rcl} S(n) & \equiv & 2S(n-1) + S(n-2) \; \equiv \; 2\big(2S(n-2) + S(n-3)\big) + S(n-2) \; \equiv \; 5S(n-2) + 2S(n-3) \\ & \equiv & S(n-2) + 2S(n-3) \equiv \; 2S(n-3) + S(n-4) + 2S(n-4) \; \equiv \; S(n-4) \;. \end{array}$ Working modulo $25$ we have a longer calculation. Leaving the details to the determined yields $S(n) \; \equiv \; 7S(n-15) \; \equiv \; 49S(n-30) \; \equiv \; -S(n-30) \; \equiv \; S(n-60)\;,$ so that $S(n) \,\equiv\, S(n-4)$ modulo $4$ and $S(n) \,\equiv\, S(n-60)$ modulo $25$ . Putting these results together yields $S(n) \,\equiv\, S(n-60)$ modulo $100$ for all $n \ge 61$ .

If $A$ is the smallest period modulo $100$ , then (Euclidean Division Algorithm) $A$ must be a factor of $60$ . Since $4$ is the smallest period modulo $4$ (modulo $4$ , the sequence is $1,3,3,1,1,3,3,1,\ldots$ ), it follows that $A$ is a multiple of $4$ . Since $S(5) = 41$ and $S(1) = 1$ , $A \neq 4$ . Since $S(2) = 3$ and $S(14) \equiv 43$ modulo $100$ , $A \neq 12$ . Since $S(21) \equiv 93$ modulo $100$ , $A \neq 20$ , and hence we deduce that $A = 60$ .

This is literally the hardest thing ever in Brilliant.

$P_{n}(x)$ is Chebyshev polynomial of the first kind.

$\displaystyle P_{n}(x) = \frac{n}{2}\displaystyle \sum\limits_{k=0}^{\lfloor\frac{n}{2}\rfloor}(-1)^{k}2^{n-2k}\frac{(n-k-1)!}{k!(n-2k)!}x^{n-2k}$ Wow.

Therefore, $S(n) = |P_{n}(1)| = \displaystyle\frac{n}{2}\displaystyle \sum\limits_{k=0}^{\lfloor\frac{n}{2}\rfloor}2^{n-2k}\frac{(n-k-1)!}{k!(n-2k)!}$

By generating the numbers, we get the sequence like this, starting from $n = 1$ . (Thank you four-function calculator.)

1, 3, 7, 17, 41, 99, 239, 577, 1393, 3363, 8119, 19601, 47321, 114243, 275807, 665857, 1607521, 3880899, 9369319, 22619537, 54608393, 131836323, 318281039, 768398401, 1855077841, 4478554083, 10812186007, 26102926097, 63018038201, 152139002499, 367296043199, 886731088897, ERROR, ERROR, .....

Seems that my calculator became a potato (and my brain too), the sequence is the same as A001333 (OEIS), which is the numerators of continued fraction that converges to $\sqrt{2}$ . Coincidentally, the sequence is also the same as the series expansion of $\displaystyle \frac{1+x}{1-2x-x^{2}}$ . Wow wow wow.

Since OEIS doesn't even give you the terms after $n = 31$ , goddammit OEIS, we should proceed the given expression.

$\displaystyle \frac{1+x}{1-2x-x^{2}} = -\frac{1+x}{(x+1-\sqrt{2})(x+1+\sqrt{2})} = \frac{1}{2}\left(\frac{1}{\sqrt{2}-1-x}+\frac{1}{-\sqrt{2}-1-x}\right)$

$= \displaystyle\frac{1}{2}\left(\displaystyle\sum\limits_{n=0}^{\infty}(1+\sqrt{2})^{n+1}x^{k}+\displaystyle\sum\limits_{n=0}^{\infty}(1-\sqrt{2})^{n+1}x^{k}\right)$

$= \displaystyle\sum\limits_{n=0}^{\infty}\frac{\left(1+\sqrt{2}\right)^{n+1}+\left(1-\sqrt{2}\right)^{n+1}}{2}x^{n} = \displaystyle\sum\limits_{n=0}^{\infty}S(n)x^{n}$

Therefore, $S(n) = \displaystyle\frac{\left(1+\sqrt{2}\right)^{n+1}+\left(1-\sqrt{2}\right)^{n+1}}{2}$

This is killing me.

The question asks for $A$ such that for all $n$ , $S(n+A) \equiv S(n) \pmod{100}$ .

From $S(n) = \displaystyle\frac{\left(1+\sqrt{2}\right)^{n+1}+\left(1-\sqrt{2}\right)^{n+1}}{2} = \frac{1}{2}\left(\displaystyle\sum\limits_{k=0}^{n+1}\binom{n}{k}\sqrt{2}^{k}+\displaystyle\sum\limits_{k=0}^{n+1}\binom{n}{k}(-1)^{k}\sqrt{2}^{k}\right)$

$= \displaystyle\frac{1}{2}\left(2\displaystyle\sum\limits_{k=0}^{\lfloor\frac{n+1}{2}\rfloor}\binom{n}{k}2^{k}\right) = \displaystyle\sum\limits_{k=0}^{\lfloor\frac{n+1}{2}\rfloor}\binom{n}{k}2^{k}$

Similarly, $S(n+A) = \displaystyle\sum\limits_{k=0}^{\lfloor\frac{n+A+1}{2}\rfloor}\binom{n+A}{k}2^{k} = \displaystyle\sum\limits_{k=0}^{\lfloor\frac{n+A+1}{2}\rfloor}\left(\displaystyle\sum\limits_{j=0}^{n}\binom{n}{j}\binom{A}{k-j}\right)2^{k} = \displaystyle\sum\limits_{k=0}^{\lfloor\frac{n+A+1}{2}\rfloor}2^{k}\displaystyle\sum\limits_{j=0}^{n}\binom{n}{j}\binom{A}{k-j}$ .............................................help.

I give up. Let's carefully look at the sequence in WolframAlpha. Input "expand (1+x)/(1-2*x-x^2)" and you will get all the terms you want. Just look at the last 2 digits on each term, and find 01. You might find earlier at $A = 11$ , but we must get to the point that the sequence repeats at $A = \boxed{60}$ .

Help me.