Trigonometry Challenge 4
sin 1 5 1 1 π − sin 1 5 π tan 3 0 1 1 π − tan 3 0 π = ?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
How is that ∑ k = 1 n cos 2 n + 1 2 n π = − 2 1 ?
Log in to reply
The following is the proof for k = 0 ∑ n − 1 cos ( 2 n + 1 2 k + 1 π ) = 2 1 . Similar proof for k = 0 ∑ n − 1 cos ( 2 n + 1 2 k π ) = − 2 1 .
S = k = 0 ∑ n − 1 cos ( 2 n + 1 2 k + 1 π ) = ℜ { k = 0 ∑ n − 1 e 2 n + 1 2 k + 1 π i } = ℜ { e 2 n + 1 π i k = 0 ∑ n − 1 e 2 n + 1 2 k π i } = ℜ { e 2 n + 1 π i ( 1 − e 2 n + 1 2 π i 1 − e 2 n + 1 2 n π i ) } = ℜ { 1 − e 2 n + 1 2 π i e 2 n + 1 π i − e π i } = ℜ ⎩ ⎨ ⎧ ( 1 + e 2 n + 1 π i ) ( 1 − e 2 n + 1 π i ) e 2 n + 1 π i + 1 ⎭ ⎬ ⎫ = ℜ { 1 − e 2 n + 1 π i 1 } = ℜ { 1 − cos 2 n + 1 π i − i sin 2 n + 1 π i 1 } = ℜ { ( 1 − cos 2 n + 1 π i ) 2 + sin 2 2 n + 1 π i 1 − cos 2 n + 1 π i + i sin 2 n + 1 π i } = ℜ { 2 − 2 cos 2 n + 1 π i 1 − cos 2 n + 1 π i + i sin 2 n + 1 π i } = 2 1
Log in to reply
Wow, so it is proved by using complex number. Thanks for explanation!
sin 1 5 1 1 π − sin 1 5 π tan 3 0 1 1 π − tan 3 0 π = 2 sin 3 0 1 1 π cos 3 0 1 1 π − 2 sin 3 0 π cos 3 0 π cos 3 0 1 1 π sin 3 0 1 1 π − cos 3 0 π sin 3 0 π = cos 3 0 1 1 π cos 3 0 π ( 2 sin 3 0 1 1 π cos 3 0 1 1 π − 2 sin 3 0 π cos 3 0 π ) sin 3 0 1 1 π cos 3 0 π − cos 3 0 1 1 π sin 3 0 π = 2 sin 3 0 1 1 π cos 3 0 π cos 2 3 0 1 1 π − 2 sin 3 0 π cos 3 0 1 1 π cos 2 3 0 π sin 3 0 ( 1 1 − 1 ) π
= ( sin 3 0 1 2 π + sin 3 0 1 0 π ) cos 2 3 0 1 1 π − ( sin 3 0 1 2 π − sin 3 0 1 0 π ) cos 2 3 0 π sin 3 0 1 0 π = ( sin 5 2 π + sin 3 π ) cos 2 3 0 1 1 π − ( sin 5 2 π − sin 3 π ) cos 2 3 0 π sin 3 π = ( sin 5 2 π + 2 3 ) cos 2 3 0 1 1 π − ( sin 5 2 π − 2 3 ) cos 2 3 0 π 2 3
= sin 5 2 π ( cos 2 3 0 1 1 π − cos 2 3 0 π ) + 2 3 ( cos 2 3 0 1 1 π + cos 2 3 0 π ) 2 3 = 2 sin 5 2 π ( cos 2 3 0 1 1 π − cos 2 3 0 π ) + 3 ( cos 2 3 0 1 1 π + cos 2 3 0 π ) 3
= 2 sin 5 2 π ( cos 3 0 1 1 π − cos 3 0 π ) ( cos 3 0 1 1 π + cos 3 0 π ) + 3 ( ( cos 3 0 1 1 π + cos 3 0 π ) 2 − 2 cos 3 0 1 1 π cos 3 0 π ) 3
= 2 sin 5 2 π ( − 2 sin ( 2 1 3 0 1 2 π ) sin ( 2 1 3 0 1 0 π ) ) ( 2 cos ( 2 1 3 0 1 2 π ) cos ( 2 1 3 0 1 0 π ) ) + 3 ( 4 cos 2 3 0 6 π cos 2 3 0 5 π − cos 3 0 1 2 π − cos 3 0 1 0 π ) 3 = − 2 sin 2 5 2 π sin 3 π + 3 ( 4 cos 2 5 π cos 2 6 π − cos 5 2 π − cos 3 π ) 3
= − 3 sin 2 5 2 π + 3 ( 3 cos 2 5 π − cos 5 2 π − 2 1 ) 3 = − sin 2 5 2 π + 3 cos 2 5 π − cos 5 2 π − 2 1 1 = 2 cos 5 4 π − 1 + 3 cos 2 5 π − 2 cos 2 5 π + 1 − 2 1 1 = 2 1 cos 5 4 π + cos 2 5 π 1 = − 2 1 cos 5 π + cos 2 5 π 1
= 4 sin 5 π cos 2 5 π − 2 sin 5 π cos 5 π 4 sin 5 π = 2 sin 5 2 π cos 5 π − sin 5 2 π 4 sin 5 π = sin 5 ( 2 + 1 ) π + sin 5 ( 2 − 1 ) π − sin 5 2 π 4 sin 5 π = sin 5 3 π + sin 5 π − sin 5 2 π 4 sin 5 π = sin 5 ( 5 − 3 ) π + sin 5 π − sin 5 2 π 4 sin 5 π
= sin 5 2 π + sin 5 π − sin 5 2 π 4 sin 5 π = sin 5 π 4 sin 5 π = 4
S = sin 1 3 2 ∘ − sin 1 2 ∘ tan 6 6 ∘ − tan 6 ∘ = 2 cos 7 2 ∘ sin 6 0 ∘ cos 6 6 ∘ sin 6 6 ∘ − cos 6 ∘ sin 6 ∘ = 2 cos 6 6 ∘ cos 6 ∘ cos 7 2 ∘ sin 6 0 ∘ sin 6 6 ∘ cos 6 ∘ − cos 6 6 ∘ sin 6 ∘ = ( cos 7 2 ∘ + cos 6 0 ∘ ) cos 7 2 ∘ sin 6 0 ∘ sin 6 0 ∘ = cos 2 7 2 ∘ + 2 1 cos 7 2 ∘ 1 = 4 cos 2 7 2 ∘ + 2 cos 7 2 ∘ 4 = 1 4 = 4
Note that since cos 7 2 ∘ = 4 5 − 1 , then 4 cos 7 2 ∘ + 1 = 5 , so 1 6 cos 2 7 2 ∘ + 8 cos 7 2 ∘ + 1 = 5 , and 4 cos 2 7 2 ∘ + 2 cos 7 2 ∘ = 1 .
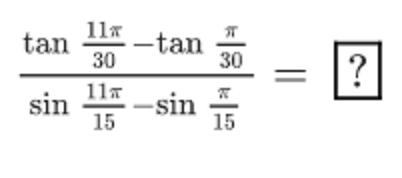

X = sin 1 5 1 1 π − sin 1 5 π tan 3 0 1 1 π − tan 3 0 π = sin ( 5 2 π + 3 π ) − sin ( 5 2 π − 3 π ) − tan 3 0 1 9 π − tan 3 0 π = 2 cos 5 2 π sin 3 π tan 3 π − ( tan 3 0 1 0 π + tan 3 0 1 9 π + tan 3 0 π ) = 3 cos 5 2 π tan 3 π − tan 3 π tan 3 0 1 9 π tan 3 0 π = cos 5 2 π 1 − cos 3 0 1 9 π cos 3 0 π sin 3 0 1 9 π sin 3 0 π = cos 5 2 π cos 3 0 1 9 π cos 3 0 π cos 3 0 1 9 π cos 3 0 π − sin 3 0 1 9 π sin 3 0 π = 2 1 cos 5 2 π ( cos 5 3 π + cos 3 2 π ) cos 3 2 π = cos 5 2 π ( − cos 5 2 π − 2 1 ) − 1 = 2 cos 2 5 2 π + cos 5 2 π 2 = cos 5 4 π + cos 5 2 π + 1 2 = − 2 1 + 1 2 = 4 Note: tan ( π − x ) = − tan x If A + B + C = π ⟹ tan A + tan B + tan C = tan A tan B tan C Note: cos ( A + B ) = cos A cos B − sin A sin B Note: cos A cos B = 2 1 ( cos ( A − B ) + cos ( A + B ) ) Note: cos ( π − x ) = − cos x Note: cos 2 x = 2 cos 2 x − 1 Note: k = 1 ∑ n cos 2 n + 1 2 k π = − 2 1
Note: k = 0 ∑ n − 1 cos ( 2 n + 1 2 k π ) = − 2 1 (see proof here ).