Trigonometry for Pros Repost

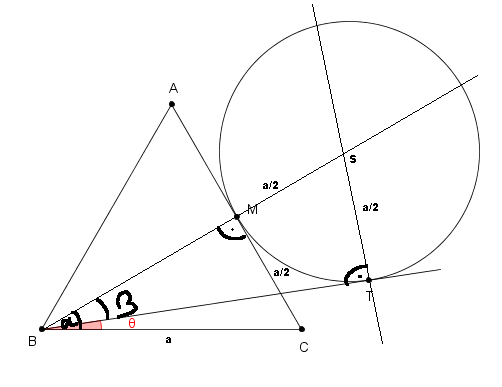
Let's start with drawing a perpendicular lines from the line BT intersecting T and from CM intersecting M. Let's call the intersection of those two lines S, which is also a center of a circle, since we know that the circle is tangent to AC at point M. Then call the CBM angle alpha.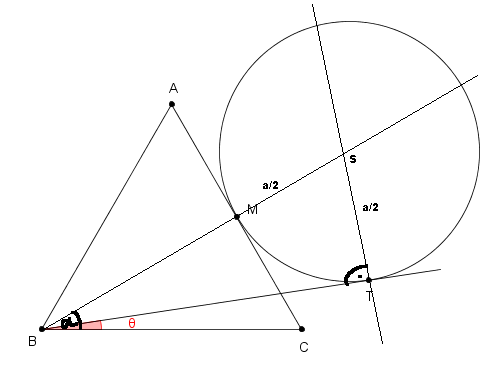 Line BM is also a height of a triangle BCA and since the triangle is equilateral, we can say that alfa = 30 degrees, since it's half of an angle CBA, which is always 60 degrees like all the angles in equilateral triangles. We can now tell, that if we knew the angle TBM, which we can call beta, we could just substract alfa from it and it will give us theta - but for that we need to know lengths of at least two sides of a right triangle BTS. We can compute height BM of a triangle BCA by using pythagorean theorem. $\left| {BM} \right| = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \sqrt {{a^2} - \frac{{{a^2}}}{4}} = \sqrt {\frac{3}{4} \times {a^2}} = a \times \frac{{\sqrt 3 }}{2}$ Now we can join |BM| + |MS| so we can get another side of a triangle BTS. $\left| {BS} \right| = \left| {BM} \right| + \left| {MS} \right| = \frac{{a \times \sqrt 3 }}{2} + \frac{a}{2} = \frac{{a \times \sqrt 3 + a}}{2} = \frac{{a \times \left( {\sqrt 3 + 1} \right)}}{2}$ After that we can just use a sin and subtract alfa from beta and compute a tan of it. $\tan \left( \theta \right) = \tan \left( {30 - \arcsin \left( {\frac{1}{{\sqrt 3 + 1}}} \right)} \right) \sim 0.149973819...$ Now we can get rid of the arcsin from tan by few simple steps. $\begin{array}{l} \tan \left( {a - b} \right) = \frac{{\tan \left( a \right) - \tan \left( b \right)}}{{1 + \tan \left( a \right) \times \tan \left( b \right)}}\\ \frac{1}{{\sqrt 3 + 1}} \times \frac{{\sqrt 3 - 1}}{{\sqrt 3 - 1}} = \frac{{\sqrt 3 - 1}}{2}\\ \tan \left( \theta \right) = \frac{{\tan \left( {30} \right) - \tan \left( {\arcsin \left( {\frac{{\sqrt 3 }}{2} - \frac{1}{2}} \right)} \right)}}{{1 + \tan \left( {30} \right) \times \tan \left( {\arcsin \left( {\frac{{\sqrt 3 }}{2} - \frac{1}{2}} \right)} \right)}}\\ \arcsin \left( {\frac{{\sqrt 3 }}{2} - \frac{1}{2}} \right) = f\\ \tan \left( \theta \right) = \frac{{\frac{1}{{\sqrt 3 }} - \tan \left( f \right)}}{{1 + \frac{1}{{\sqrt 3 }} \times \tan \left( f \right)}} = \frac{{\frac{{1 - \sqrt 3 \tan \left( f \right)}}{{\sqrt 3 }}}}{{\frac{{\sqrt 3 + \tan \left( f \right)}}{{\sqrt 3 }}}} = \frac{{\sqrt 3 \times \left( {1 - \sqrt 3 \tan \left( f \right)} \right)}}{{\sqrt 3 \times \left( {\sqrt 3 + \tan \left( f \right)} \right)}} = \frac{{1 - \sqrt 3 \tan \left( f \right)}}{{\sqrt 3 + \tan \left( f \right)}}\\ \arcsin \left( x \right) = 2 \times \arctan \left( {\frac{x}{{1 + \sqrt {1 - {x^2}} }}} \right)\\ f = \arcsin \left( {\frac{{\sqrt 3 - 1}}{2}} \right) = 2 \times \arctan \left( {\frac{{\frac{{\sqrt 3 - 1}}{2}}}{{1 + \sqrt {1 - {{\left( {\frac{{\sqrt 3 - 1}}{2}} \right)}^2}} }}} \right) = 2 \times \arctan \left( {\frac{{\sqrt 3 - 1}}{{2 + 2 \times \sqrt {1 - \frac{{4 - 2\sqrt 3 }}{4}} }}} \right) = 2 \times \arctan \left( {\frac{{\sqrt 3 - 1}}{{2 + 2 \times \sqrt {1 - \frac{{2 - \sqrt 3 }}{2}} }}} \right)\\ f = 2 \times \arctan \left( {\frac{{\sqrt 3 - 1}}{{2 + 2 \times \sqrt {\frac{{\sqrt 3 }}{2}} }}} \right)\\ g = \frac{{\sqrt 3 - 1}}{{2 + 2 \times \sqrt {\frac{{\sqrt 3 }}{2}} }}\\ \tan \left( {2x} \right) = \frac{{2 \times \tan \left( x \right)}}{{1 - {{\tan }^2}\left( x \right)}}\\ f = \tan \left( {2 \times \arctan \left( g \right)} \right) = \frac{{2 \times \tan \left( {\arctan \left( g \right)} \right)}}{{1 - {{\tan }^2}\left( {\arctan \left( g \right)} \right)}} = \frac{{2 \times g}}{{1 - {g^2}}} = \frac{{\frac{{\sqrt 3 - 1}}{{1 + \sqrt {\frac{{\sqrt 3 }}{2}} }}}}{{1 - {{\left( {\frac{{\sqrt 3 - 1}}{{2 + 2 \times \sqrt {\frac{{\sqrt 3 }}{2}} }}} \right)}^2}}}\\ {g^2} = \frac{{4 - 2 \times \sqrt 3 }}{{4 + 8 \times \sqrt {\frac{{\sqrt 3 }}{2}} + 2 \times \sqrt 3 }} = \frac{{2 - \sqrt 3 }}{{2 + \sqrt 3 + 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} }}\\ 1 - {g^2} = \frac{{2 + \sqrt 3 + 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} - 2 + \sqrt 3 }}{{2 + \sqrt 3 + 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} }} = \frac{{2\sqrt 3 + 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} }}{{2 + \sqrt 3 + 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} }}\\ \tan \left( f \right) = \frac{{\sqrt 3 - 1}}{{1 + \sqrt {\frac{{\sqrt 3 }}{2}} }} \times \frac{{2 + \sqrt 3 + 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} }}{{2\sqrt 3 + 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} }} = \frac{{2 \times \sqrt 3 + 3 + 4 \times \sqrt 3 \times \sqrt {\frac{{\sqrt 3 }}{2}} - 2 - \sqrt 3 - 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} }}{{2\sqrt 3 + 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} + \sqrt {\frac{{\sqrt 3 }}{2}} \times 2\sqrt 3 + 4 \times \frac{{\sqrt 3 }}{2}}} = \frac{{1 + \sqrt 3 + 4 \times \sqrt 3 \times \sqrt {\frac{{\sqrt 3 }}{2}} - 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} }}{{2 \times \sqrt 3 + 2 \times \sqrt {\frac{{\sqrt 3 }}{2}} \times \left( {2 + \sqrt 3 } \right) + 4 \times \frac{{\sqrt 3 }}{2}}}\\ \tan \left( f \right) = \frac{{1 + \sqrt 3 + 4 \times \sqrt 3 \times \sqrt {\frac{{\sqrt 3 }}{2}} - 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} }}{{2 \times \sqrt 3 + 2 \times \sqrt {\frac{{\sqrt 3 }}{2}} \times \left( {2 + \sqrt 3 } \right) + 4 \times \frac{{\sqrt 3 }}{2}}} = \frac{{1 + \sqrt 3 + 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} \times \left( {\sqrt 3 - 1} \right)}}{{4 \times \sqrt 3 + 2 \times \sqrt {\frac{{\sqrt 3 }}{2}} \times \left( {2 + \sqrt 3 } \right)}} = \frac{{1 + \sqrt 3 + 4 \times \sqrt {\frac{{\sqrt 3 }}{2}} \times \left( {\sqrt 3 - 1} \right)}}{{2 \times \left( {2 \times \sqrt 3 + \sqrt {\frac{{\sqrt 3 }}{2}} \times \left( {2 + \sqrt 3 } \right)} \right)}}\\ \tan \left( \theta \right) = \frac{{1 - \sqrt 3 \times \tan \left( f \right)}}{{\sqrt 3 + \tan \left( f \right)}} = \frac{{1 - \sqrt 3 \left( {\frac{{1 + \sqrt 3 + 4\sqrt 3 \sqrt {\frac{{\sqrt 3 }}{2}} - 4\sqrt {\frac{{\sqrt 3 }}{2}} }}{{2\sqrt 3 + 2\sqrt {\frac{{\sqrt 3 }}{2}} \left( {2 + \sqrt 3 } \right) + 4\frac{{\sqrt 3 }}{2}}}} \right)}}{{\sqrt 3 + \frac{{1 + \sqrt 3 + 4\sqrt 3 \sqrt {\frac{{\sqrt 3 }}{2}} - 4\sqrt {\frac{{\sqrt 3 }}{2}} }}{{2\sqrt 3 + 2\sqrt {\frac{{\sqrt 3 }}{2}} \left( {2 + \sqrt 3 } \right) + 4\frac{{\sqrt 3 }}{2}}}}} = \frac{{1 - \sqrt 3 \left( {\frac{{1 + \sqrt 3 + 4\sqrt {\frac{{\sqrt 3 }}{2}} \left( {\sqrt 3 - 1} \right)}}{{2\left( {2\sqrt 3 + \sqrt {\frac{{\sqrt 3 }}{2}\left( {2 + \sqrt 3 } \right)} } \right)}}} \right)}}{{\sqrt 3 + \left( {\frac{{1 + \sqrt 3 + 4\sqrt {\frac{{\sqrt 3 }}{2}} \left( {\sqrt 3 - 1} \right)}}{{2\left( {2\sqrt 3 + \sqrt {\frac{{\sqrt 3 }}{2}\left( {2 + \sqrt 3 } \right)} } \right)}}} \right)}}\\ \phi = \frac{{1 + \sqrt 3 + 4\sqrt {\frac{{\sqrt 3 }}{2}} \left( {\sqrt 3 - 1} \right)}}{{4\sqrt 3 + 2\sqrt {\frac{{\sqrt 3 }}{2}\left( {2 + \sqrt 3 } \right)} }}\\ \tan \left( \theta \right) = \frac{{1 - \sqrt 3 \times \phi }}{{\sqrt 3 + \phi }} \end{array}$