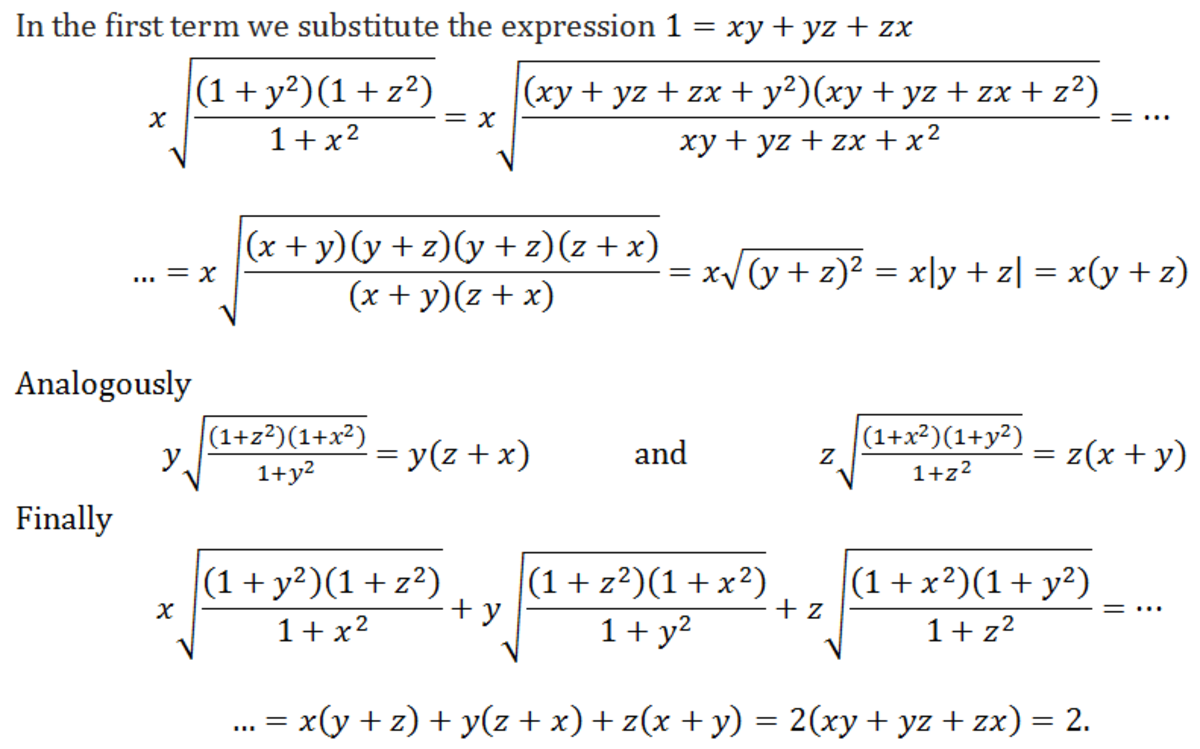Trigonometry in Algebra 3

Algebra Level 4

x ( 1 + y 2 ) ( 1 + z 2 ) 1 + x 2 + y ( 1 + z 2 ) ( 1 + x 2 ) 1 + y 2 + z ( 1 + x 2 ) ( 1 + y 2 ) 1 + z 2 x \sqrt{ \dfrac{(1+y^2)(1+z^2)}{1+x^2}} + y \sqrt{ \dfrac{(1+z^2)(1+x^2)}{1+y^2}} + z \sqrt{ \dfrac{(1+x^2)(1+y^2)}{1+z^2}}

Given that x , y x,y and z z are positive reals satisfying x y + x z + y z = 1 xy + xz + yz = 1 , evaluate the expression above.

This problem is part of this set .


The answer is 2.00.

Tín Phạm Nguyễn by Tín Phạm Nguyễn , 26, Vietnam

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Darío Sb
Mar 25, 2015

11 Helpful 0 Interesting 0 Brilliant 0 Confused
Jun Arro Estrella
Dec 26, 2015

Since x , y x, y and z z are in the domain of positive integers,

One can assume that x = y = z x = y = z where x , y , z x,y,z are all positive :)

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Kumar Krish
Jan 13, 2019

Put x=tanA, y=tanB, z=tanC So tanA. tanB+tanB.tanC+tanC.tanA=1
Thus A+B+C=π/2 also 2A+2B+2C =π. So on further simplification we get Sin2A+sin2B+sin2C in numerator and in denominator 2.cosA.cosB.cosC And we know that in a triangle sin2A + sin2B + sin2C =4 cosA. cosB. cosC Thus we get the answer 2

0 Helpful 0 Interesting 0 Brilliant 0 Confused

I just let x=y=z=(1/3)^(1/2), then substitute to the given expression..

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...