Trigonometry is Fun 3 :)
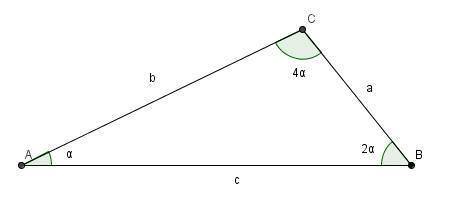 In
△
A
B
C
,
∠
C
=
4
∠
A
and
∠
B
=
2
∠
A
.
In
△
A
B
C
,
∠
C
=
4
∠
A
and
∠
B
=
2
∠
A
.
What is the value of a 2 b 2 − b c ?
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Please use the LaTeX formatting. I have edited the question, you edit the solution please. Wrap your math terms in \ ( ........ \ )
Use LaTeX code \cos for the cosine, \angle \triangle for the signs of angle and triangle respectively, \frac{a}{b} for fraction a/b etc.
Log in to reply
i don't know how to apply LaTex in Solutions.. :(
Log in to reply
I told you, wrap your Math Codes in the \ ( ........... \ ) .
Just like, when you type \text{ \ ( x^y , \frac{x}{y} \ )} , it will appear as x y , y x
Solution 1:
By Letting:
x = angle A
2x = Angle B
4x = Angle C
By Law of sines,
a/(sin A) = b/(sin B) = c/(sin C)
= a/(sin x) = b/(sin 2x) = c/(sin 4x)
So,,
b/a = (sin 2x)/(sin x) = {[2(sin x)(cos x)]}/(sin x) = 2(cos x)
c/b = (sin 4x)/(sin 2x) = {[2(sin 2x)(cos 2x)]}/(sin 2x) = 2(cos 2x) = 2[(cos^2)(x) - (sin^2)(x)]
Therefore,
(b/a)^2 - (c/b)
= {[2(cos x)]^2} - {2[(cos^2)(x) - (sin^2)(x)]}
= [4(cos^2)(x)] - {2[(cos^2)(x) - (sin^2)(x)]}
= [4(cos^2)(x)] - [2(cos^2)(x) - 2(sin^2)(x)]
= 2(cos^2)(x) + 2(sin^2)(x)
= 2
Final Answer: 2
Solution 2:
a=2RsinA,b=2RsinB,c=2RsinC
sin^2(B)/sin^2(A)-sinC/sinB
substituting the values and using the identity sin 2X=2sinX cos X in both fractions we get
4cos^2(A)-2cos2A
=4cos^2(A)-2(2cos^2(A)-1)=2
; where in, R is the Circum-radius
Solution 3:
By law of sines,
b/a = sin(2A)/sin(A) = 2*cos(A) and
c/b = sin(4A)/sin(2A) = 2*cos(2A).
Thus,
(b/a)^2 - c/b
= 4 * cos^2(A) - 2 * cos(2A)
= 4 * cos^2(A)- [4*cos^(A)-2]
= 2..