Trigonometry or Square completing?

Geometry Level 3

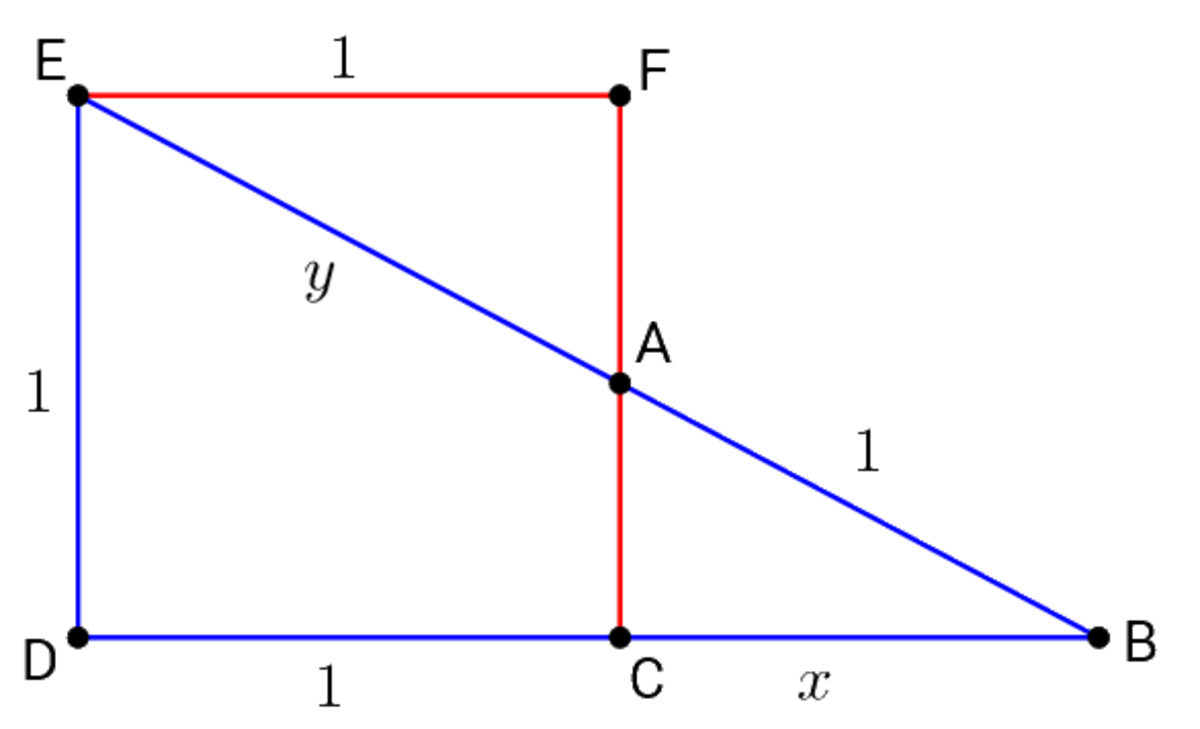
In the diagram above, the blue right triangle is partially overlapping the 1 × 1 1\times1 red square, sharing a corner. If A B ‾ = 1 \overline{AB}=1 and B C ‾ = x , \overline{BC}=x, find x x to 3 decimal places.


The answer is 0.883.

View wiki
Vitor Santos by Vitor Santos , 21, Brazil

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Andy Hayes
Feb 1, 2017

Define the remaining points in the figure as below:

It can be seen that △ A B C ∼ △ A E F . \triangle ABC \sim \triangle AEF. Then y = 1 x . y=\frac{1}{x}. Apply the Pythagorean Theorem on △ E B D : \triangle EBD:

( x + 1 ) 2 + 1 2 = ( 1 + 1 x ) 2 x 2 + 2 x + 2 = 1 + 2 x + 1 x 2 x 4 + 2 x 3 + x 2 − 2 x − 1 = 0 \begin{aligned} (x+1)^2+1^2 &= \left(1+\frac{1}{x}\right)^2 \\ \\ x^2+2x+2 &= 1+\frac{2}{x}+\frac{1}{x^2} \\ \\ x^4+2x^3+x^2-2x-1 &= 0 \end{aligned}

Edit : See @Mark Hennings comment for how to solve this quartic. The only positive root to the equation above is:

x = 1 2 ( − 1 + 2 + 2 2 − 1 ) ≈ 0.883 . \begin{aligned} x &= \frac{1}{2}\left(-1+\sqrt{2}+\sqrt{2\sqrt{2}-1}\right) \\ \\ &\approx \boxed{0.883}. \end{aligned}

5 Helpful 0 Interesting 0 Brilliant 0 Confused

We can write x 4 + 2 x 3 + x 2 − 2 x − 1 = 0 ( x 2 + x + 1 ) 2 = 2 ( x + 1 ) 2 x 2 + x + 1 = ± 2 ( x + 1 ) x 2 + ( 1 ∓ 2 ) x + ( 1 ∓ 2 ) = 0 ( x + 1 2 ( 1 ∓ 2 ) ) 2 = 1 4 ( 1 ∓ 2 ) 2 − ( 1 ∓ 2 ) = 1 4 ( 1 ∓ 2 ) ( − 3 ∓ 2 ) \begin{aligned} x^4 + 2x^3 + x^2 - 2x - 1 & = 0 \\ (x^2 + x + 1)^2 & = 2(x + 1)^2 \\ x^2 + x + 1 & = \pm\sqrt{2}(x+1) \\ x^2 + (1 \mp \sqrt{2})x + (1 \mp \sqrt{2}) & = 0 \\ \big(x + \tfrac12(1 \mp \sqrt{2})\big)^2 & = \tfrac14(1 \mp \sqrt{2})^2 - (1 \mp \sqrt{2}) \; = \; \tfrac14(1 \mp \sqrt{2})(-3 \mp \sqrt{2}) \end{aligned} For a real root x x , we must choose the sign to make the RHS positive. Thus ( x + 1 2 ( 1 − 2 ) ) 2 = 1 4 ( 2 − 1 ) ( 3 + 2 ) = 1 4 ( 2 2 − 1 ) x + 1 2 ( 1 − 2 ) = ± 1 2 2 2 − 1 \begin{aligned} \big(x + \tfrac12(1 - \sqrt{2})\big)^2 & = \tfrac14(\sqrt{2}-1)(3+\sqrt{2}) \; = \;\tfrac14(2\sqrt{2} - 1) \\ x + \tfrac12(1 - \sqrt{2}) & = \pm\tfrac12\sqrt{2\sqrt{2}-1} \end{aligned} and we now pick the positive root.

A monic quartic can always be written in the form ( x 2 + a x + b ) 2 + c ( x + d ) 2 (x^2 + ax + b)^2 + c(x + d)^2 for some constants a , b , c , d a,b,c,d . Thus a quartic equation can be solved by first taking square roots, and then solving a pair of quadratics. In general you have to be able to solve a cubic equation to determine these four constants, but in this case it was easy.

Mark Hennings - 4 years, 4 months ago

Log in to reply

Awesome, thanks :)

Andy Hayes - 4 years, 4 months ago

You can plot any equation using this tool. https://www.desmos.com/calculator

Vijay Simha - 4 years, 4 months ago

Log in to reply

You also can plot any equation using this tool "Wolfram" (search in Google Play)

I Gede Arya Raditya Parameswara - 4 years, 4 months ago

I tried by taking x= cosδ and converted it into a quadratic in terms of trigonometric terms but I am getting 0.468.I don't know what is wrong with my method.

Dhanvanth Balakrishnan - 4 years, 4 months ago
Raj Mantri
Feb 24, 2017

It can be seen that Triangle BED ~ Triangle BAC

S o , B C / B D = A C / E D So, BC / BD = AC / ED

x/(x+1) = [ √ ( A B ) 2 − ( B C ) 2 ] / 1 [√{(AB)^2 - (BC)^2} ] /1

x = ( x + 1 ) ( √ 1 − x 2 ) x = (x+1)(√1-x^2)

Squaring both sides

x 2 = ( x + 1 ) 2 ( 1 − x 2 ) x^2 = (x+1)^2 (1-x^2)

x 2 = ( x 2 + 2 x + 1 ) ( 1 − x 2 ) x^2 = (x^2+2x+1)(1-x^2)

x 2 = x 2 + 2 x + 1 − x 4 − 2 x 3 − x 2 x^2 = x^2+2x+1- x^4 - 2x^3- x^2

x 2 = 2 x + 1 − x 4 − 2 x 3 x^2 = 2x+1- x^4 - 2x^3

0 = 2 x + 1 − x 4 − 2 x 3 − x 2 0 = 2x + 1 - x^4 - 2x^3 - x^2

Solve this Quartic for x. The only root positive root to above equation is

x = 0.883 x =0.883

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Since △ A B C △ A E F \triangle ABC ~ \triangle AEF it follows that A F = C F = 1 2 AF=CF= \frac{1} {2} which makes the triangles 30-60-90 triangles and so x = 1 2 3 x = \frac{1} {2} \sqrt {3}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

△ A B C \triangle ABC and △ A E F \triangle AEF are similar, not congruent. Your method is good for getting an estimate, since they are so close to being congruent. Note that the exact value is a little bit off:

Estimate: 1 2 3 ≈ 0.866. Actual: 1 2 ( − 1 + 2 + 2 2 − 1 ) ≈ 0.883. \begin{array}{rrl} \text{Estimate: } & \frac{1}{2}\sqrt{3} & \approx 0.866. \\ \text{Actual: } & \frac{1}{2}\left(-1+\sqrt{2}+\sqrt{2\sqrt{2}-1}\right) & \approx 0.883. \end{array}

Andy Hayes - 4 years, 4 months ago

Log in to reply

It did take my answer as correct. But if I look at the picture again my reasoning should lead to a contradiction... So my answer is o deed faulty

Peter van der Linden - 4 years, 4 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...