Trigonometry Practise
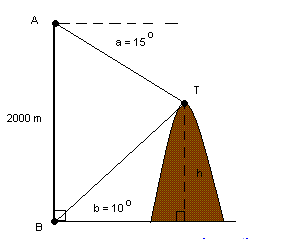 When the top T of a mountain is viewed from point A, 2000 m from ground, the angle of depression a is equal to 15 degrees and when it is viewed from point B on the ground the angle of elevation b is equal to 10 degrees . If points A and B are on the same vertical line, find the height h of the mountain. (round answer to one decimal place).
When the top T of a mountain is viewed from point A, 2000 m from ground, the angle of depression a is equal to 15 degrees and when it is viewed from point B on the ground the angle of elevation b is equal to 10 degrees . If points A and B are on the same vertical line, find the height h of the mountain. (round answer to one decimal place).
The answer is 793.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
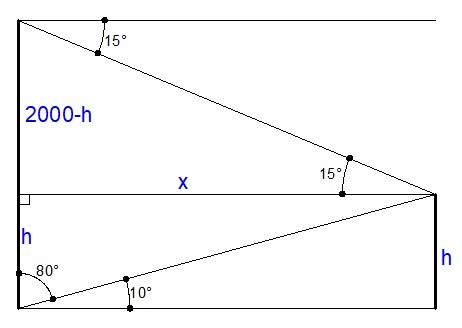
let x be the horizontal distance from the viewer to the mountain.
tan 1 0 = x h
tan 1 5 = x 2 0 0 0 − h
equate the values of x and solve for h
tan 1 0 h = tan 1 5 2 0 0 − h
h = 7 9 3 . 7 7
 tan
1
5
=
x
2
0
0
0
−
h
or
x
tan
1
5
=
2
0
0
0
−
h
(
1
)
tan
1
5
=
x
2
0
0
0
−
h
or
x
tan
1
5
=
2
0
0
0
−
h
(
1
)
tan 8 0 = h x or x = tan 8 0 ( 2 )
Substitute ( 2 ) in ( 1 ) . We have
h tan 8 0 ( tan 1 5 ) = 2 0 0 0 − h
h + 1 . 5 1 9 6 h = 2 0 0 0
2 . 5 1 9 6 h = 2 0 0 0
h ≈ 7 9 3 . 8
from the figure as shown. tan(10) = h / d
tan(15) = (2000 - h) / d Solve for d the last 2 equations as follows
d = h / tan(10) and d = (2000 - h) / tan(15) and eliminate d as follows
h / tan(10) = (2000 - h) / tan(15) Solve the above for h
h = 2000 tan(10) / [ tan(15) + tan(10)]
= 793.8 m