Trigonometry Products

Let $w=e^{2\pi{i}/n}$ . Now $\prod_{k=1}^{n-1}(1+2\cos(2\pi{k}/n))=\prod_{k=1}^{n-1} (1+w^k+w^{-k})$ $= \prod_{k=1}^{n-1}(w^{2k}+w^k+1)=\prod_{k=1}^{n-1}\left(\frac{w^{3k}-1}{w^k-1}\right)$ $=\frac{\prod_{k=1}^{n-1}(w^{3k}-1)}{\prod_{k=1}^{n-1}(w^k-1)}=1$ .

In the last quotient, the products in the numerator and denominator are the same, since both $w^k$ and $w^{3k}$ run through all $n$ th roots of unity (other than 1).

Now $\prod_{k=1}^{n}(1+2\cos(2\pi{k}/n))=\boxed{3}$ since $k=n$ produces the factor 3.

The last term of the sum if $3$ , hence the sum is:

$S=3\displaystyle \prod_{k=1}^{n-1}\left(1+2\cos \dfrac{2\pi k}{n}\right)$

Now, as Tanishq Varshney says, we use the identity $1+2\cos 2\theta=\frac{\sin 3\theta}{\sin \theta}$ :

$S=3\displaystyle \prod_{k=1}^{n-1}\left(\dfrac{\sin \frac{3\pi k}{n}}{\sin \frac{\pi k}{n}}\right)$

Note that the number of negative terms in the denominator is the same than the ones in the denominator. Now, let $w=e^{2 \pi i/n}$ . Note that also $w^3$ is a primitive $n$ th root of unity. Also $|1-w^k|=2\left|\sin\dfrac{\pi k}{n}\right|$

Now, let $P(x)=\dfrac{x^n-1}{x-1}=(x-w)(x-w^2)\cdots(x-w^{n-1})=(x-w^3)(x-w^6)\cdots(x-w^{3(n-1)})$

But also, $P(x)=x^{n-1}+x^{n-2}+\cdots+x+1$

By letting $x=1$ and applying absolute value to both sides, we obtain:

$n=|1-w||1-w^2|\cdots|1-w^{n-1}|=|1-w^3||1-w^6|\cdots|1-w^{3(n-1)}|$

Finally, with the identity stated above:

$S=3\times\dfrac{|1-w^3||1-w^6|\cdots|1-w^{3(n-1)}|}{|1-w||1-w^2|\cdots|1-w^{n-1}|}$

$S=\boxed{3}$

Use the algebraic expression, 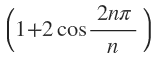then cancel n, 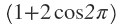since 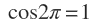then the remaining numbers are (1+2) therefore, the result is 3.

put n=5 as n is any prime number and then use values of cos(pi/5) and cos(2pi/5) and solve