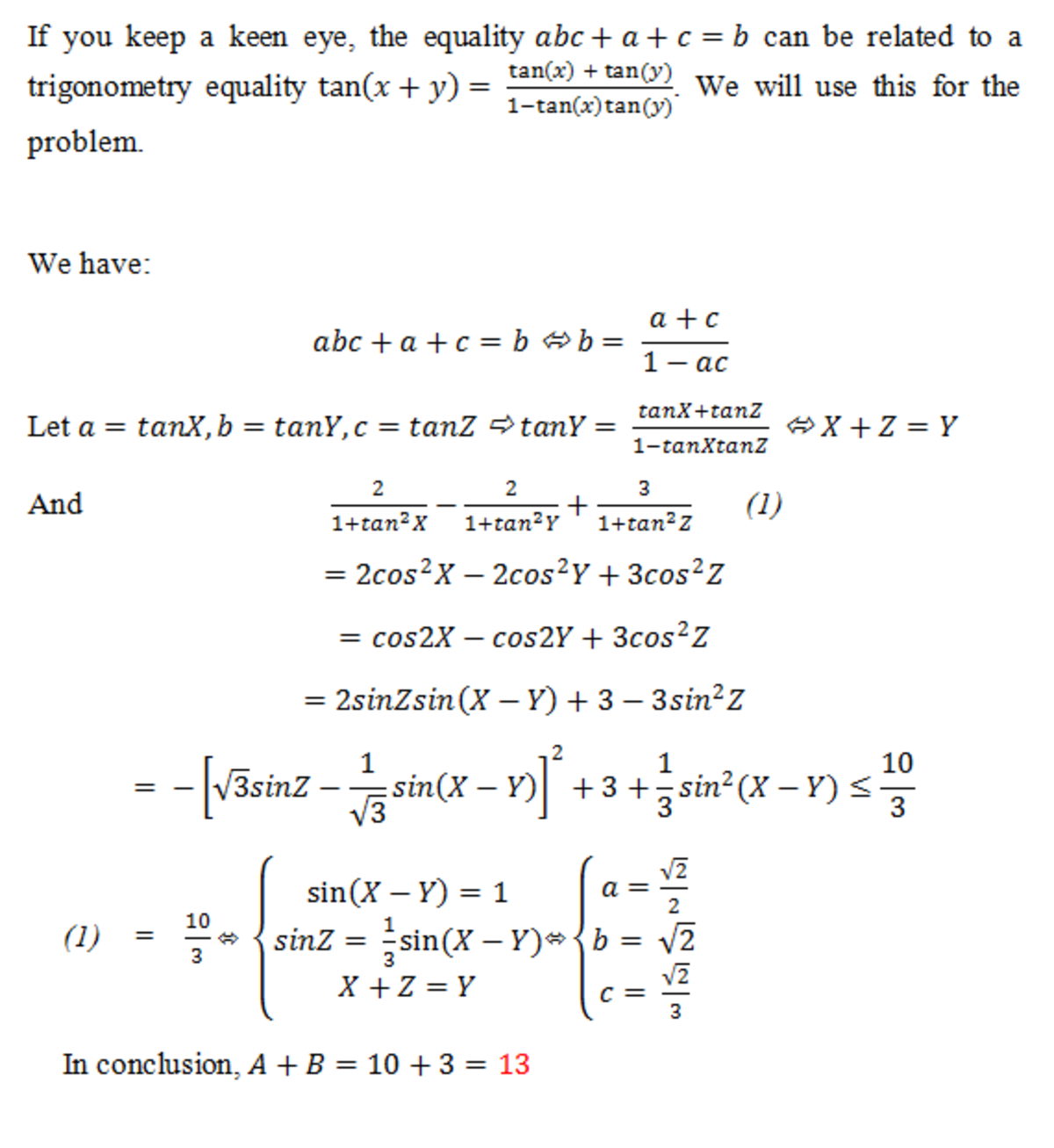Trigonometry Related

Geometry Level 5

$\dfrac{2}{a^2 + 1} - \dfrac{2}{b^2 + 1} + \dfrac{3}{c^2 + 1}$

Given that $a,b$ and $c$ are positive real numbers satisfying $abc + a + c = b$ . If the maximum value of the expression above can be expressed as $\dfrac AB$ for coprime positive integers $A$ and $B$ , find the value of $A+B$ .

The answer is 13.

2 solutions

Leah Smith
Nov 28, 2015

I don't know how to write Latex so I will capture my DOCUMENT.

Cool problem ! Care to share some more of this type ?

Raven Herd - 5 years, 6 months ago

Thank you! I hope I will find a similar kind of problem very soon!

Leah Smith - 5 years, 6 months ago

same solution

Aakash Khandelwal - 5 years, 5 months ago

I thought most people would do the conventional methods but bravo to you *

Leah Smith - 5 years, 5 months ago

I think something is wrong. At first I didn't know what, but after re-reading it, I suspect you meant $\sin (X+Y)$ in the last few lines rather than $\sin (X-Y)$ .

But aside from that minor issue, this is a very good problem and solution.

Peter Byers - 5 years, 6 months ago

Andong Cao
Dec 2, 2015

You can also use Lagrange Multipliers to solve this problem :)

What's that ?

Raven Herd - 5 years, 6 months ago

In response to Raven Herd: It is the most popular method to calculate extrema for functions with more arguments if there are restrictions for them given by additional conditions. For information please consult the internet! ;-)

Andreas Wendler - 5 years, 6 months ago

I did but I didn't get it from wikipedia can you tell me from where I can learn it ? Thanks.

Raven Herd - 5 years, 6 months ago

Trigonometry Related

The answer is 13.

2 solutions

0 pending reports