Sine or Cosine Rule?
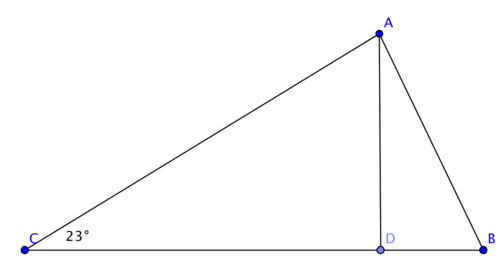 In
Δ
A
B
C
,
A
D
is the altitude from
A
. Given
b
>
c
,
∠
C
=
2
3
∘
and
A
D
=
b
2
−
c
2
a
b
c
, find
∠
B
. Enter your answer in degrees.
In
Δ
A
B
C
,
A
D
is the altitude from
A
. Given
b
>
c
,
∠
C
=
2
3
∘
and
A
D
=
b
2
−
c
2
a
b
c
, find
∠
B
. Enter your answer in degrees.
This problem is part of the set Trigonometry .
Details and Assumptions
- The picture above is not up to scale.
The answer is 113.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
Interesting approach and observation!
First, by the Cosine rule, we have that
c 2 = a 2 + b 2 − 2 a b cos ( 2 3 ∘ ) ⟹ b 2 − c 2 = a ( 2 b cos ( 2 3 ∘ ) − a )
∣ A D ∣ = b 2 − c 2 a b c = 2 b cos ( 2 3 ∘ ) − a b c .
Now since A D is an altitude we have that ∣ A D ∣ = b sin ( 2 3 ∘ ) , so
b sin ( 2 3 ∘ ) = 2 b cos ( 2 3 ∘ ) − a b c ⟹ c = 2 b sin ( 2 3 ∘ ) cos ( 2 3 ∘ ) − a sin ( 2 3 ∘ ) .
Now we also have that b sin ( 2 3 ∘ ) = ∣ A D ∣ = c sin ( ∠ B ) , so now we have
c = 2 c sin ( ∠ B ) cos ( 2 3 ∘ ) − a sin ( 2 3 ∘ )
⟹ c ( 2 sin ( ∠ B ) cos ( 2 3 ∘ ) − 1 ) = a sin ( 2 3 ∘ )
⟹ c a = sin ( 2 3 ∘ ) 2 sin ( ∠ B ) cos ( 2 3 ∘ ) − 1 .
But by the Sine rule we know that c a = sin ( 2 3 ∘ ) sin ( ∠ A ) , and so
2 sin ( ∠ B ) cos ( 2 3 ∘ ) − 1 = sin ( ∠ A ) = sin ( 1 5 7 ∘ − ∠ B )
⟹ 2 sin ( ∠ B ) cos ( 2 3 ∘ ) − 1 = sin ( 2 3 ∘ ) cos ( ∠ B ) + cos ( 2 3 ∘ ) sin ( ∠ B )
⟹ sin ( ∠ B ) cos ( 2 3 ∘ ) − cos ( ∠ B ) sin ( 2 3 ∘ ) = 1 ⟹ sin ( ∠ B − 2 3 ∘ ) = 1
⟹ ∠ B − 2 3 ∘ = 9 0 ∘ ⟹ ∠ B = 1 1 3 ∘ .
Note that ∠ B > 9 0 ∘ , so the diagram is a bit deceptive, but I don't think unfair. :)
A D = b sin ( C )
⇒ b sin ( C ) = b 2 − c 2 a b c
⇒ sin ( C ) = b 2 − c 2 a c = sin 2 ( B ) − sin 2 ( C ) sin ( A ) sin ( C ) = sin ( B + C ) sin ( B − C ) sin ( A ) sin ( C ) = sin ( A ) sin ( B − C ) sin ( A ) sin ( C ) = sin ( B − C ) sin ( C )
⇒ sin ( B − C ) = 1
⇒ B − C = 9 0 ∘
B = 1 1 3 ∘
A solution with sine rule: Using sine rule and area we can easily obtain: A D = 2 R b c = b 2 − c 2 a b c ⟹ a b 2 − c 2 = 2 R where R is the circumradius of A B C . If ∠ B is acute or right, then a b 2 − c 2 = C D − B D = 2 R ≤ C D which is clearly absurd. Hence D must lie outside of segment C B , and a b 2 − c 2 = C D + B D = 2 R . Let B ′ be the other point on line B C such that D B = D B ′ ; thus C B ′ = 2 R and A B = A B ′ . By sine rule again the circumradii of A B C , A B ′ C are the same, which forces ∠ C A B ′ = 9 0 ∘ ⟹ ∠ B = 9 0 + ∠ C = 1 1 3 ∘