Sine and Cosine ratios
sin 2 ( A ) sin 2 ( 3 A ) − cos 2 ( A ) cos 2 ( 3 A ) = 2
⟹ cos ( 2 A ) = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
Great!
I just used sin^2(a)+cos^2(a)=1 then completely it became simple. Double angle formula was much more simpler
Yup I too did it the same way.Great....
An easier method..... Sin2(3A)/sin2(A) - cos23A/cosA=2 LHS =(3sinA-4sin3A)2/sin2A - (4cos3A-3cosA)2/cos2A =sin2A(3-4sin2A)2/sin2A - cos2A(4cos2A-3)2/cos2A =(3-4sinA)2 – (4cos2A-3)2 =(3-4 sin sq.A + 4cos sq.A-3)(3-4sin sq.A-4cos sq.A + 3) =4(cos sq.A-sin sq.A)(6-4) 4(cos2A)(2)=2 Cos2A=1/4
Log in to reply
Triple Angle Formula... That was what Pi Han Goh's solution is based on too...
Log in to reply
Ohh... I didn't see it.. :P I just solved my way and posted the soln. I didn't see Pi Han's soln.
Recall the triple angle identities: sin ( 3 A ) = − 4 sin 3 A + 3 sin A , cos ( 3 A ) = 4 cos 3 A − 3 cos A .
For simplicity sake, let s = sin ( A ) , c = cos ( A ) , so s 2 + c 2 = 1 and we want to find c 2 − s 2 .
( − 4 s 2 + 3 ) 2 − ( 4 c 2 − 3 ) 2 1 6 ( s 4 − c 4 ) − 2 4 ( s 2 − c 2 ) 1 6 ( s 2 − c 2 ) ( s 2 + c 2 ) − 2 4 ( s 2 − c 2 ) ( 1 6 − 2 4 ) ( s 2 − c 2 ) c 2 − s 2 = = = = = 2 2 2 2 − 1 6 − 2 4 2 = 4 1
Moderator note:
Yes. Triple Angle Identities is a simple approach.
sin 2 A sin 2 3 A − cos 2 A cos 2 3 A = 2 ⇒ sin 2 A cos 2 A sin 2 3 A cos 2 A − cos 2 3 A sin 2 A = 2 ⇒ ( sin 3 A cos A − cos 3 A sin A ) ( sin 3 A cos A + cos 3 A sin A ) = 2 sin 2 A cos 2 A ⇒ sin 2 A sin 4 A = 2 1 sin 2 2 A ⇒ 2 sin 2 2 A cos 2 A = 2 1 sin 2 2 A ⇒ cos 2 A = 4 1
Moderator note:
The use of difference of squares to compound angle formula nailed the problem. Well done.
I just loved your Solution!
Using Euler's formula we obtain:
e i 3 θ = ( e i θ ) 3 ⟹ c o s ( 3 θ ) + i s i n ( 3 θ ) = ( c o s θ + i s i n θ ) 3 =
c o s 3 θ + 3 c o s 2 θ s i n θ i − 3 c o s θ s i n 2 θ − s i n 3 θ i
⟹ c o s ( 3 θ ) = c o s 3 θ − 3 c o s θ s i n 2 θ = c o s θ ( c o s 2 θ − 3 s i n 2 θ ) =
2 1 ∗ c o s θ ( 1 + c o s ( 2 θ ) − 3 ( 1 − c o s ( 2 θ ) ) =
c o s θ ( 2 c o s ( 2 θ ) − 1 )
s i n 3 θ = s i n θ ( 3 c o s 2 θ − s i n 2 θ ) = s i n θ ( 2 c o s ( 2 θ ) + 1 )
⟹ 2 = ( 2 c o s ( 2 A ) + 1 ) 2 − ( 2 c o s ( 2 A ) − 1 ) 2 = 8 c o s ( 2 A ) ⟹
c o s ( 2 A ) = 4 1
The triple angle and double angle identities give sin 3 A = ( sin A ) ( 3 − 4 sin 2 A ) = ( sin A ) ( 2 cos 2 A + 1 ) and cos 3 A = ( cos A ) ( 4 cos 2 A − 3 ) = ( cos A ) ( 2 cos 2 A − 1 ) .
Thus ( sin A sin 3 A ) 2 − ( cos A cos 3 A ) 2 = ( 2 cos 2 A + 1 ) 2 − ( 2 cos 2 A − 1 ) 2 = 8 cos 2 A = 2 and cos 2 A = 4 1
Moderator note:
The addition of double angle identities certainly did simplify the work. Great job!
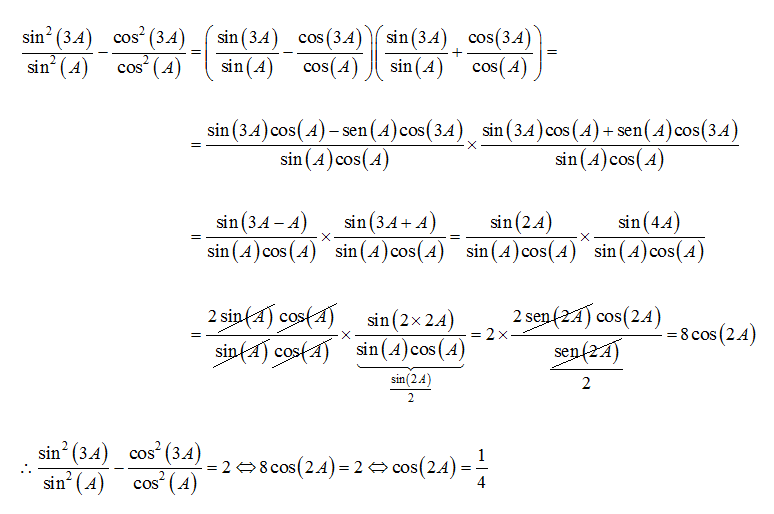
L . H . S . = s i n 2 ( A ) s i n 2 ( 3 A ) − c o s 2 ( A ) c o s 2 ( 3 A )
= s i n 2 ( A ) . c o s 2 ( A ) s i n 2 ( 3 A ) . c o s 2 ( A ) − c o s 2 ( 3 A ) . s i n 2 ( A )
= s i n 2 ( A ) . c o s 2 ( A ) [ s i n ( 3 A ) . c o s ( A ) − c o s ( 3 A ) . s i n ( A ) ] . [ s i n ( 3 A ) . c o s ( A ) + c o s ( 3 A ) . s i n ( A ) ]
Using the identities : ( i ) s i n ( A ± B ) = s i n A . c o s B ± c o s A . s i n B & ( i i ) s i n ( 2 θ ) = 2 . s i n θ . c o s θ
= s i n 2 ( A ) . c o s 2 ( A ) s i n ( 3 A − A ) . s i n ( 3 A + A ) = s i n 2 ( A ) . c o s 2 ( A ) s i n ( 2 A ) . s i n ( 4 A )
= s i n 2 ( A ) . c o s 2 ( A ) s i n ( 2 A ) . ( 2 . s i n ( 2 A ) . c o s ( 2 A ) )
= s i n 2 ( A ) . c o s 2 ( A ) 8 . s i n 2 ( A ) . c o s 2 ( A ) . c o s ( 2 A ) = 8 . c o s ( 2 A )
R . H . S . = 2
⇒ 8 . c o s ( 2 A ) = 2 ⇒ c o s ( 2 A ) = 4 1
:D