Trine University Mathematics Competition 2018 Advanced Problem #5
With credit to the authors of the Trine University Mathematics Competition of 2018,
There is a kite inscribed within a square. Lengths AD = BD = CD, and EB = BF. Find the value of angle .
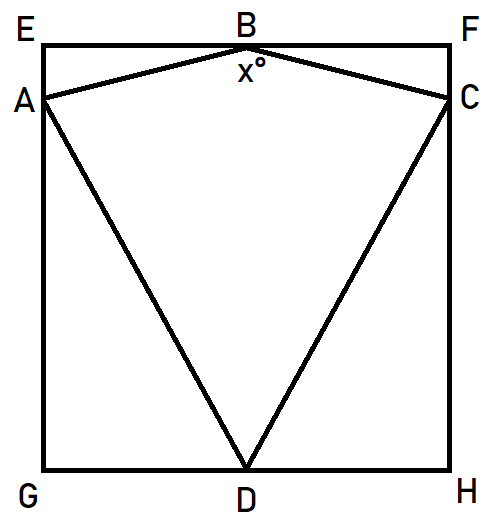
The answer is 150.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since AD = BD = CD, it can be proven that length AC = AD = BD = CD, since it is the side length of the square, and thusly the length of BD.
Given this, triangle ACD is equilateral, making all angles in the triangle 60°, and thusly angle BDC 30°.
In this triangle, since BD and CD are of the same length, it is an isosceles triangle, meaning angle DBC and DCB are equivalent.
From angle BDC equalling 30, the other angles must equal 1 8 0 − 3 0 = 1 5 0 , which split equally between both angles is 75°.
Since x° is angle ABD + CBD, and both triangles ABD and CBD are congruent, angle ABD is also 75°, making x° 7 5 + 7 5 = 1 5 0 .