Triangle/Hexagon
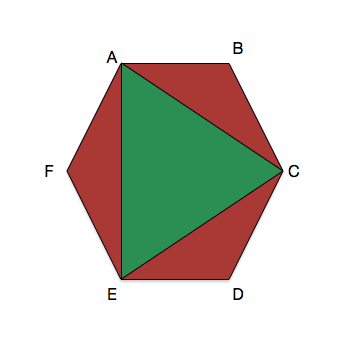 Let ABCDEF be a regular hexagon. What's the ratio of the areas of the triangle ACE to that of the hexagon ABCDEF?
Let ABCDEF be a regular hexagon. What's the ratio of the areas of the triangle ACE to that of the hexagon ABCDEF?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
22 solutions
Hehehehe... This is what I did... Great!!
excellent n easy to understand
excellent idea..........
awesome solution.....u deserve an upvote!
very nice approach..! Creative!
very nice solution.... to think that I used 5 pages of paper just to solve it using trigonometry....
I dint understand...
Exactly what I did
Excellent answer, superior to mine except that you should change 'whoch' to 'which'!
Let O be the center of the hexagon. Draw lines A O , C O , and E O .
The answer is obvious now: 2 1
very good solution
nice solution ..
Elegant solution :)
Total side( A to F) =6(red) Green side=3( A,C,E) Ratio=green side/total side of the hexagon = 3/6=1/2
question is asked about area not the perimeter
nice solution...
Let O be the center of hexagon . Here the areas of triangles ABC ,AOC , AOE ,AFE ,COE and CDE are equal and let the area be x Area of Hexagon is sum of areas of all triangles .Thus the area is 6x While area of triangle ACE is sum of areas of triangles AOC ,COE ,AOE .So the area will be 3x Now,the ratio of the areas of the trangle ACE to that of the hexagon ABCDEF is 3x/6x=1/2
Imagine the outer triagle be a same triagle.
Good answer, but put an 'n' in 'triangle' and I think you might mean by 'a same triangle' 'an inner formed by connecting the center of the hexagon to the ends of the hypotenuse of each outer triangle, then compare the areas'?
Join triangles AFE, ABC, and EDC to make an equilateral triangle AEC. You can do this because the largest angle in each of these triangles is 120 degrees and the sides are all equal in length. Since EC is the length of the side of ACE as well as AEC, the equilateral triangles have the same area. The area of the hexagon is the sum of these areas, so the ratio of the area of AEC (call it A) to the hexagon is A / (A + A) = 1/2.
Just imagine each of the lines AC, CE and EA betwixt red and green areas is like a planar mirror that reflects the red isoceles triangles like A-B-C into their green reflections like A-C- hexagon center .
Now we can see the red area and the green area total three congruent isoceles triangles each and if we remember Euclid, he will remind us that he would reckon the green and red areas equal and the green area to sum up to one half the total area enclosed within the perimeter of the hexagon A-B-C-D-E-F-A.
Joining AD,BE,CF,we finf insecting point G,where AGE,AGC,CFG are triangles with similar areas of AFG,CDE and ABC ,therefore area of trianle ACE is 1/2 of hexagonal ABCDEF Ans K.K.GARG,India
If you draw lines from A to D, B to E, and C to F, it forms six triangles. Each triangle is half red and half green, problem solved :)
how I did this was just by seeing the three little triangles CDE, ABC, and AEF. if all of those are able to fit inside the triangle ACE then, well it would just make sense from my point of view
let each side=a, for regular hexagon each angle is 120,
area of AEF = 1/2xaxaxsin120 =0.433a^2, thus the 3 red triangular area= 1.29a^2
imagine a perpendicular FX on AE from F, angle AFD=60, so for triangle AFD,
sin60=AD/a,
=>AD=0.86a
so,AE=AC=EC=2x0.86a
now, area of AEC= 1/2x1.72ax1.72a xsin60=1.29a^2
area AEC : area ABCDEF=1:2
clearly visualising the picture we can conclude dt its a regular hexagon.....where the green shaded region consists of 3 triangles of same area.....in total we thus get 6 triangles in the hexagon.....thus area(triangle) / area(hexagon) =3/6 = 1/2....dts it......
((n-2)*180 )= will give angle of any polygon ,, so triangle / hexagon = 1/2
i soved this problem with imagination only
if we fold the red wings there it occupies all the green area .....so its obviously 1/2
every angle in the regular hexagon equal 120 deg. and the sides are equal too so the solution is
A(ABCDEF)=A(ABC)+A(CDE)+A(AEF)+A(AEC)/
A(ABC)=A(CDE)=A(AEF)/
AE=AC=CE/
A(ACE)=A(ABC)+A(CDE)+A(AEF)/
A(ACE)=1/2 A(ABCDEF) .
as ABCDEF is a regular hexagon imagine a circle subscribing it. then the ratio of areas simply depends on the number of sides of a polygon.
WLOG, let AB = 1. Since B = (6-2) 180/6 = 120, AMB is a 30-60-90 triangle where M is the midpoint of AC. So AM = sqrt(3)/2 and AC = 2 AM = sqrt(2). The hexagon can be divided into 6 equilateral triangles of side 1. Therefore the desired ratio is [sqrt(3)/1]^2/6 = 1/2.
Just, Fold the out side(red area) inside the green area of the triangle. ;)
Imagination is more important than knowledge! -Einstein
what are you fighting for?
If you try to fill the green triangle with the red ones, it can be seen that's half.
Sketch a hexagon and label each angle consequently with the alphabets suggested. Then draw a line two line connecting AE and CE. From there 4 simmilar triangles are derived from the sketch. The area constricted with the lines consist of two 2 triangles and the whole hexagon has four.ghhjjjjj2
Imagine folding the sides inward...whoch fill the triangle...As simple as that !