Trio of Triangles

Geometry Level 3

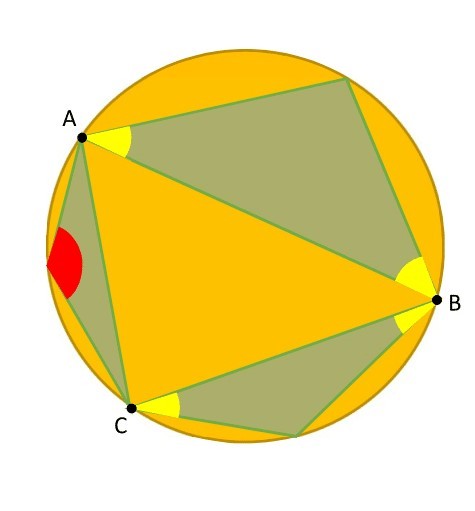Triangle ABC has three other triangles attached to it so that their remaining vertices are located on the circumcircle of triangle ABC. Depending on the shape of the original triangle, what relationships may exist between the measure of the red angle, R, and the sum of the yellow angles, S.

There are cases when R<S but not cases when R>S There are cases when R>S but not cases when R<S R has to be equal S There are cases when R>S as well as cases when R<S

1 solution

Victor Paes Plinio
Jan 3, 2018

Relevant Wiki: Circle Inscribed Angle

By the Inscribed Angle Theorem, the red angle measures half of the angle formed by the arc $AC$ .

The arc $AC$ is the sum of the arcs $AM$ , $MB$ , $BN$ and $NC$ .

By the Inscribed Angle Theorem the yellow angles $1$ , $2$ , $3$ , and $4$ measure half of the angles formed by the arcs $MB$ , $AM$ , $NC$ and $BN$ respectively.

Hence, we can conclude that if the red angle is half of the angle formed by the arc $AC$ and the yellow angles are half of the angles formed by the arcs that compose the big arc $AC$ , then the sum of the yellow angles is equal to the red angle.

Boa Victor !! Resolvi do mesmo jeito

Relue Tamref - 3 years, 5 months ago

Trio of Triangles

1 solution

0 pending reports