Triple Tan
⎣ ⎡ tan 2 α tan 2 β + 8 + tan 2 β tan 2 γ + 8 + tan 2 γ tan 2 α + 8 ⎦ ⎤ 2
Triangle A B C has angles α , β , γ . What is the maximum value of the expression above.
The answer is 75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
We claim that if a,b,c are angles of a triangle, then tan(a/2)tan(b/2)+tan(b/2)tan(c/2)+tan(c/2)tan(a/2)=1.square root[(x+8)(y+8)]+square roof[(y+8)(z+8)]+square root[(z+8)(x+8)]}.
Using a+b+c=180, the addition formulas and the fact that tan x = cot(90-x), we have
tan(c/2)=cot((a+b)/2)=(1-(tan(a/2))(tan(b/2)))/(tan(a/2)+tan(b/2))---------(I)
By plugging in (I) into the left hand side of the claim to complete the proof of the claim.
Let x=tan(a/2), y=tan(b/2), z=tan(c/2).
The given formula will transform into (square root(x+8)+square root(y+8)+square root(z+8))^2 where x+ y+z=1.
Simplifying, the given formula will become 25+2{square root[(x+8)(y+8)]+square roof[(y+8)(z+8)]+square root[(z+8)(x+8)]}.
By Cauchy-Schwarz inequality and using the fact that x+y+z=1,
square root[(x+8)(y+8)]+square root[(y+8)(z+8)]+square root[(z+8)(x+8)] <= square root{[(x+8)+(y+8)+(z+8)][(y+8)+(z+8)+(x+8)]}=25.
The given formula is smaller than or equal to 25+2(25)=75.
Equality occurs when alpha=beta=gamma=60 degrees.
Please use Latex!!!!!!
First, we show that tan 2 α tan 2 β + tan 2 β tan 2 γ + tan 2 γ tan 2 α = 1 . This follows because
tan 2 α ( tan 2 β + tan 2 γ ) = tan 2 α ( tan 2 β + tan 2 γ ) × 1 − tan 2 β tan 2 γ 1 − tan 2 β tan 2 γ = tan 2 α tan 2 β + γ ( 1 − tan 2 β tan 2 γ ) = 1 − tan 2 β tan 2 γ
Hence, by AM-GM (or Cauchy-Schwarz), we know that ( A + B + C ) 2 ≤ 3 ( A + B + C ) , so the expression is less than or equal to 3 ( tan 2 α tan 2 β + 8 + tan 2 β tan 2 γ + 8 + tan 2 γ tan 2 α + 8 ) = 7 5 .
Equality holds when A = B = C = 3 2 π .
i solved this problem using Titu's lemma it is much easier
Log in to reply
Great! Can you add your solution?
By standard identities: sin 2 1 α = b c ( s − b ) ( s − c ) cos 2 1 α = b c s ( s − a ) (and similarly), so that tan 2 1 α = s ( s − a ) ( s − b ) ( s − c ) and similarly. Thus tan 2 1 α tan 2 1 β = s s − c and similarly. We are being asked to maximize (over all triangles) ( 9 − a + b + c 2 a + 9 − a + b + c 2 b + 9 − a + b + c 2 c ) 2 This (by a simple application of Cauchy-Schwarz) has a maximum value of 7 5 when a = b = c .
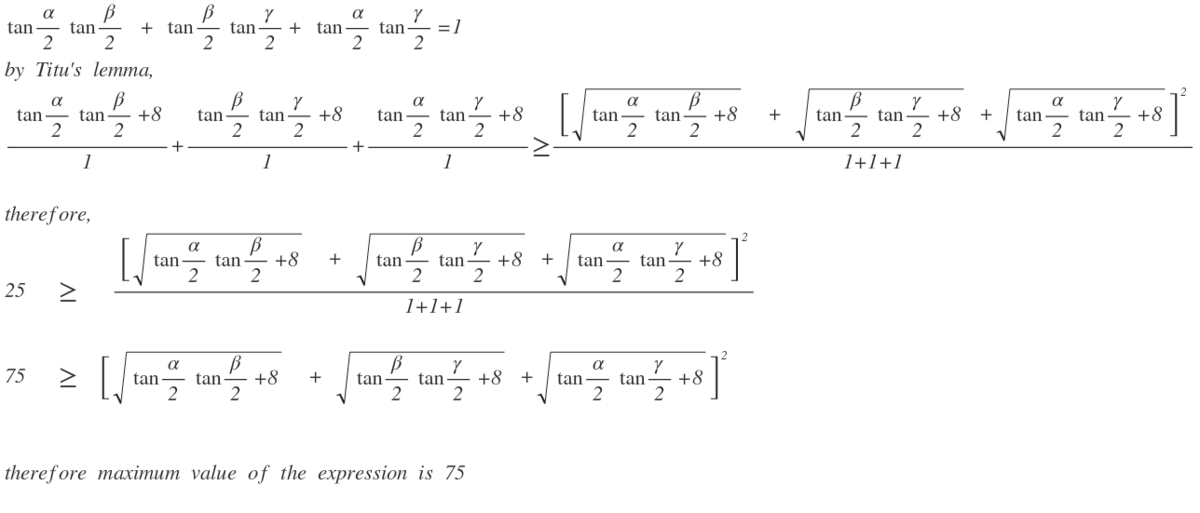
Firstly, since α + β + γ = 1 8 0 , then 2 α + β + γ = 9 0
Since tan ( 2 α + β ) = cot 2 γ , we know tan ( 2 α + 2 β ) ∗ tan 2 γ = 1 . we will get 1 − tan 2 α × tan 2 β tan 2 α + tan 2 β × tan 2 γ = 1 , which reduces to
tan 2 α × tan 2 β + tan 2 β × tan 2 γ + tan 2 α × tan 2 γ = 1
Let a = tan 2 α × tan 2 β + 8 , b = tan 2 γ × tan 2 β + 8 , c = tan 2 α × tan 2 γ + 8 .
We know a + b + c = 1 + 8 + 8 + 8 = 2 5
Let X be a + b + c , X 2 = a + b + c + 2 × a b + 2 × b c + 2 × a c
Since we are looking for the maximum value, using AM GM inequality, we get : X 2 ≤ a + b + c + a + b + b + c + c + a = 7 5 .
In this case, the maximum value is obtained when a = b = c which reduced to α = β = γ = 6 0 ∘ .