Triples and Areas!
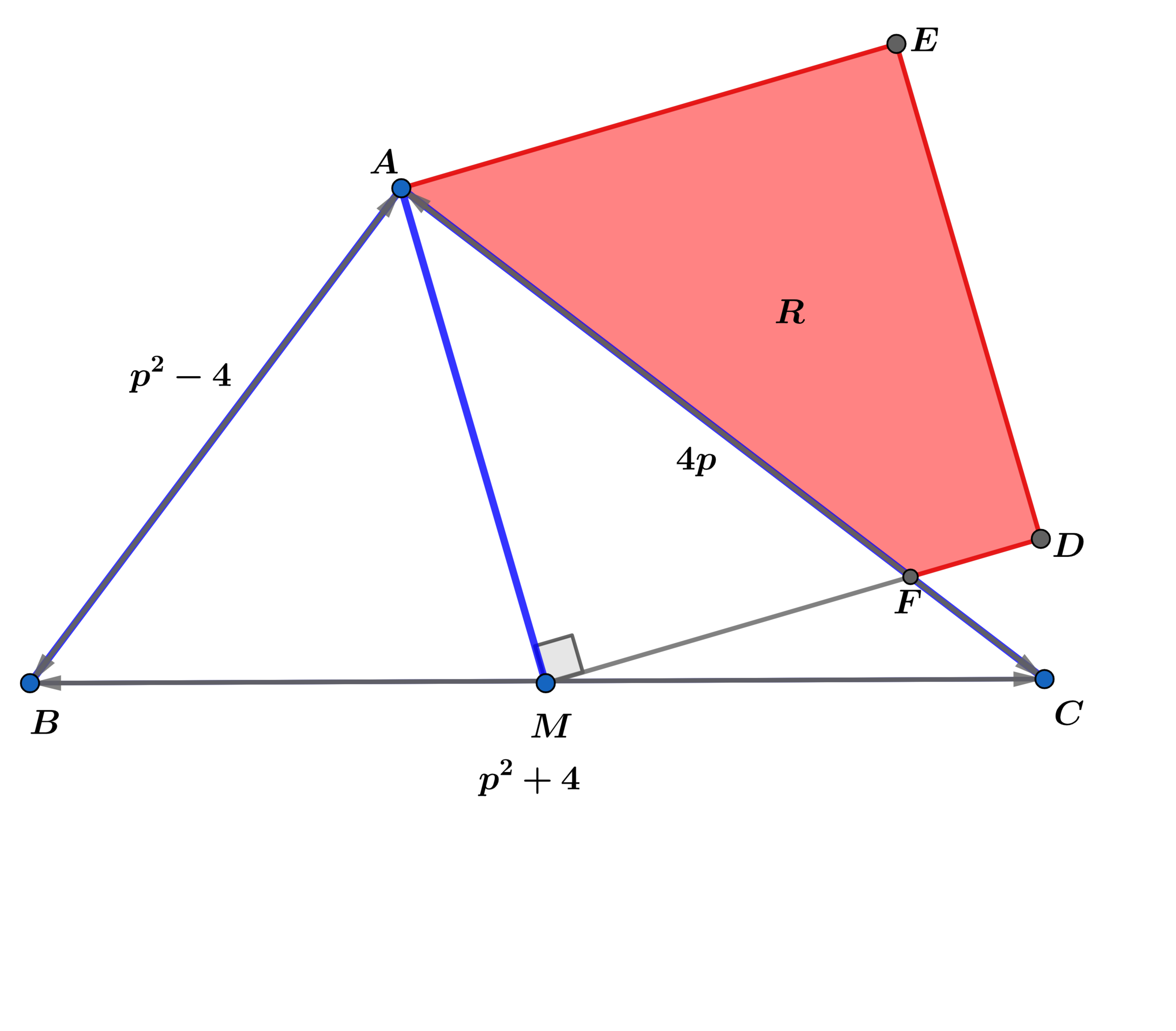
Let p be positive integer and p > 2 .
In △ A B C , A B = p 2 − 4 , A C = 4 p , B C = p 2 + 4 , M is a midpoint of B C and A M is a side of square M A E D and M D intersects A C at F .
Find A A E D F using the largest value of the integer p for which M D intersects A C at F .
I . E ; Find A A E D F using the largest value of the integer p for which the above construction is possible.
The answer is 62.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice Approach. You found integer p m a x = 4 , then used this value to obtain A A D E F , which is somewhat easier then first finding A A D E F = f ( p ) , then finding the integer p m a x = 4 and then evaluating f ( 4 ) .
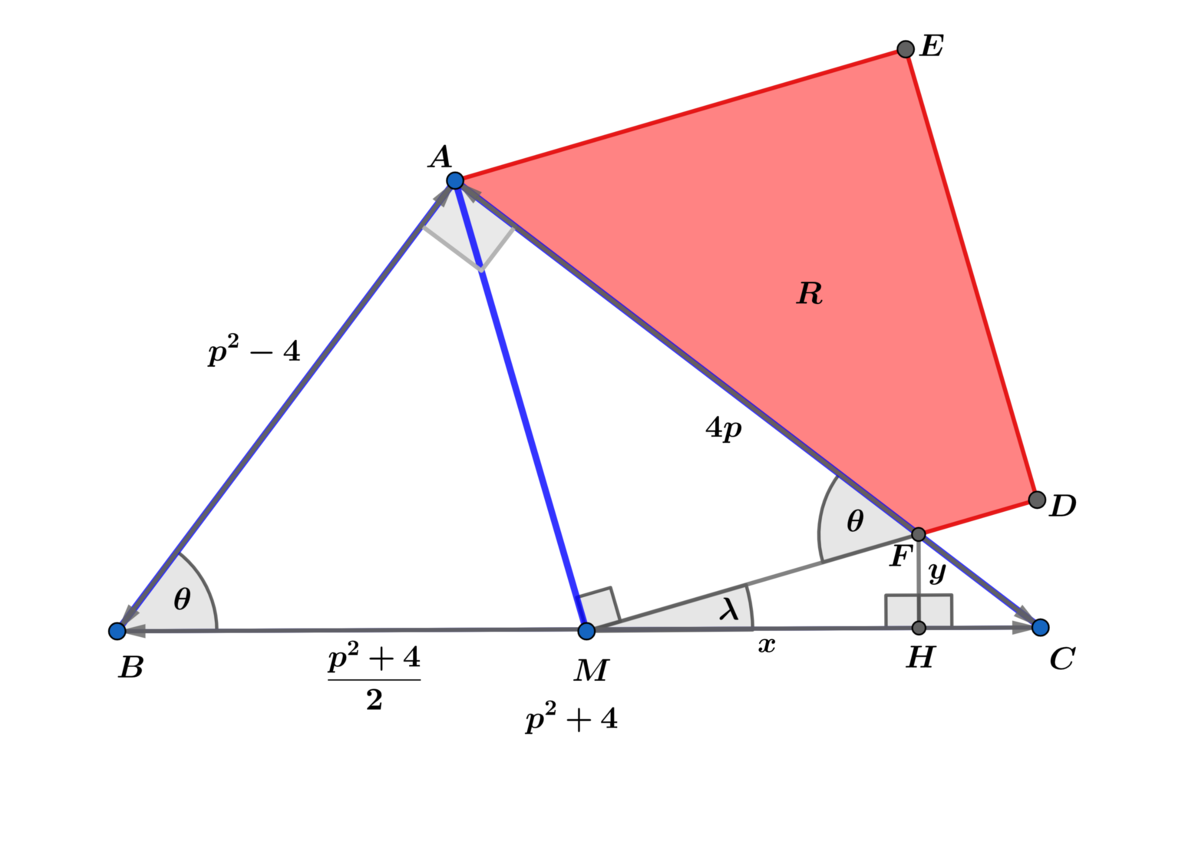
Let p > 2 .
( p 2 − 4 , 4 p , p 2 + 4 ) is a Pythagorean triple ⟹ △ A B C is a right triangle with m ∠ A = 9 0 ∘ and cos ( θ ) = p 2 + 4 p 2 − 4 .
Using the law of cosines on △ B A M with included ∠ A B C = θ ⟹
A M 2 = ( p 2 − 4 ) 2 + 4 p 2 + 4 − 2 ( p 2 − 4 ) ( 2 p 2 + 4 ) ( p 2 + 4 p 2 − 4 ) ⟹ A M = 4 p 2 + 4
⟹ M F = A F cos ( θ ) = p 2 + 4 p 2 − 4 A F ⟹ 4 ( p 2 + 4 ) 2 + ( p 2 + 4 ) 2 ( p 2 − 4 ) 2 A F 2 = A F 2
⟹ 4 ( p 2 + 4 ) 2 = ( p 2 + 4 ) 2 1 6 p 2 A F 2 ⟹ A F 2 = 6 4 p 2 ( p 2 + 4 ) 4 ⟹ A F = 8 p ( p 2 + 4 ) 2
⟹ M F = 8 p ( p 2 + 4 ) ( p 2 − 4 ) ⟹ A △ A M F = 3 2 p ( p 2 + 4 ) 2 ( p 2 − 4 ) ⟹
A A E D F = A R = A A E D M − A △ A M F = 3 2 p ( p 2 + 4 ) 2 ( 8 p − p 2 + 4 ) .
To find the largest integer value of p we need slope m M F > 0 .
λ = 2 θ − 9 0 ∘ ⟹ m M F = tan ( 2 θ − 9 0 ∘ ) = sin ( 2 θ ) − cos ( 2 θ ) = 2 sin ( θ ) cos ( 2 θ ) sin 2 ( θ ) − cos 2 ( θ ) =
8 p ( p 2 − 4 ) ( p − 2 ) 2 ( 4 + 4 p − p 2 ) > 0 and we already have p > 2 ⟹
p 2 − 4 p − 4 < 0 ⟹ p = ⌊ 2 ( 2 + 1 ) ⌋ = 4 ⟹ ( 2 < p ≤ 4 )
and using p m a x = 4 ⟹ A R = 2 1 2 5 = 6 2 . 5
Note: If p was a prime with p > 2 we have Primitive Pythagorean Triples and p = 3 is the only prime that satisfies the above construction and the unique solution A R = 9 6 3 2 1 1 .
As long as A B < A C , the M D will intersect A C . Therefore, p 2 − 4 < 4 p , which solves to 2 − 2 2 < p < 2 + 2 2 or − 0 . 8 2 8 < p < 4 . 8 2 8 , which makes p = 4 the largest positive integer value of p .
If p = 4 , then A B = p 2 − 4 = 4 2 − 4 = 1 2 , A C = 4 p = 4 ⋅ 4 = 1 6 , and B C = p 2 + 4 = 4 2 + 4 = 2 0 .
Since 1 2 2 + 1 6 2 = 2 0 2 , △ A B C is a right triangle, and by Thales's Theorem right ∠ A will lie on the circle that has B C as its diameter.
Since M is the midpoint of B C , M is the center of that circle, and M B = M A = M C = 1 0 , so △ A C M is an isosceles triangle.
As two base angles of an isosceles triangle, ∠ M C A = ∠ M A C , which means △ A M F ∼ △ C A B by AA similarity.
Since △ A M F ∼ △ C A B , M F = M A ⋅ A C A B = 1 0 ⋅ 1 6 1 2 = 2 1 5 .
Then A A E D F = A M A E D − A △ A M F = A M 2 − 2 1 ⋅ M F ⋅ A M = 1 0 2 − 2 1 ⋅ 2 1 5 ⋅ 1 0 = 2 1 2 5 = 6 5 . 2 .