Triples and Areas!
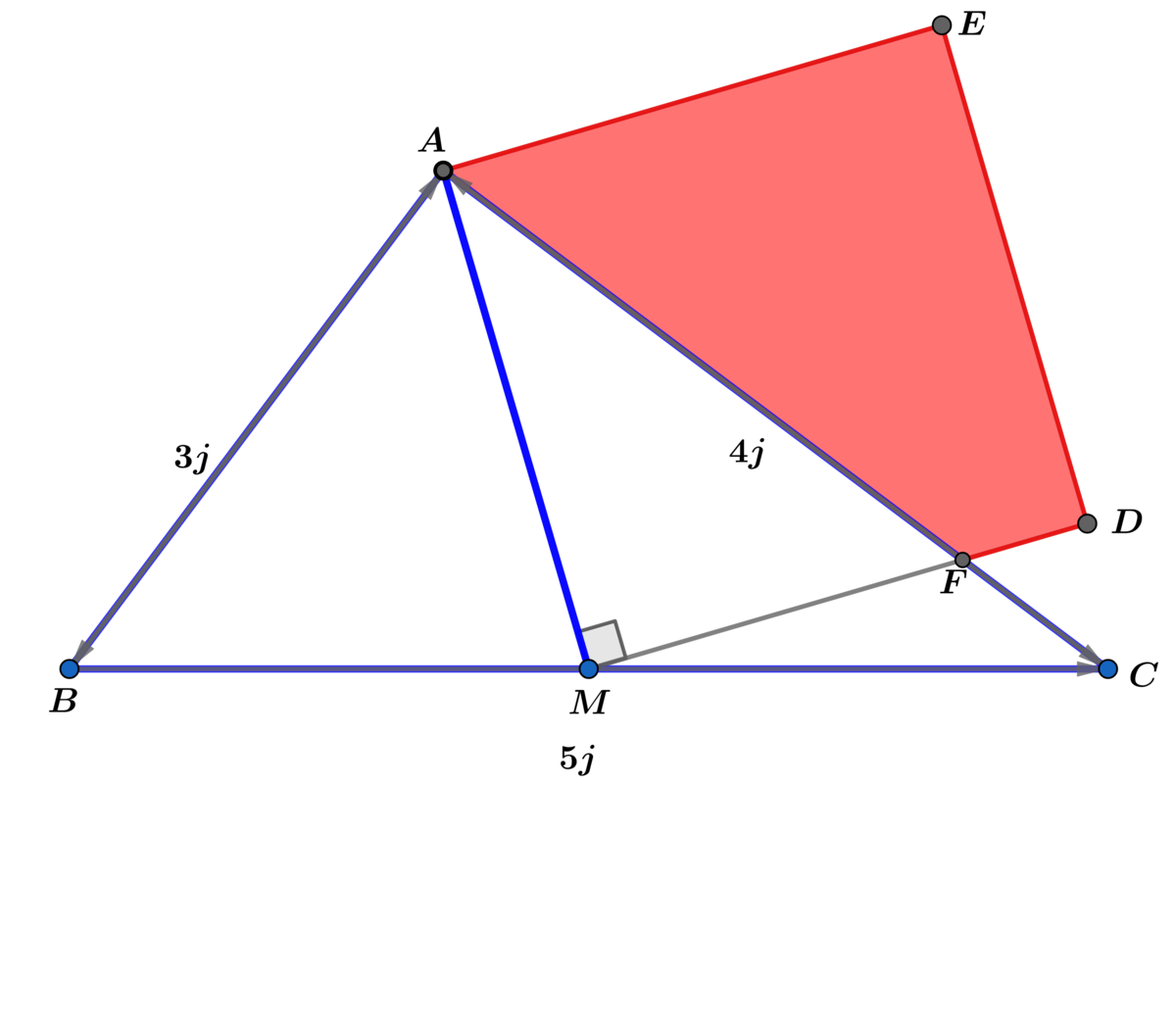
In △ A B C , A B = 3 j , A C = 4 j , B C = 5 j , M is a midpoint of B C and A M is a side of square M A E D .
Find the integer value of j for which A A E D F = 2 5 0 .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
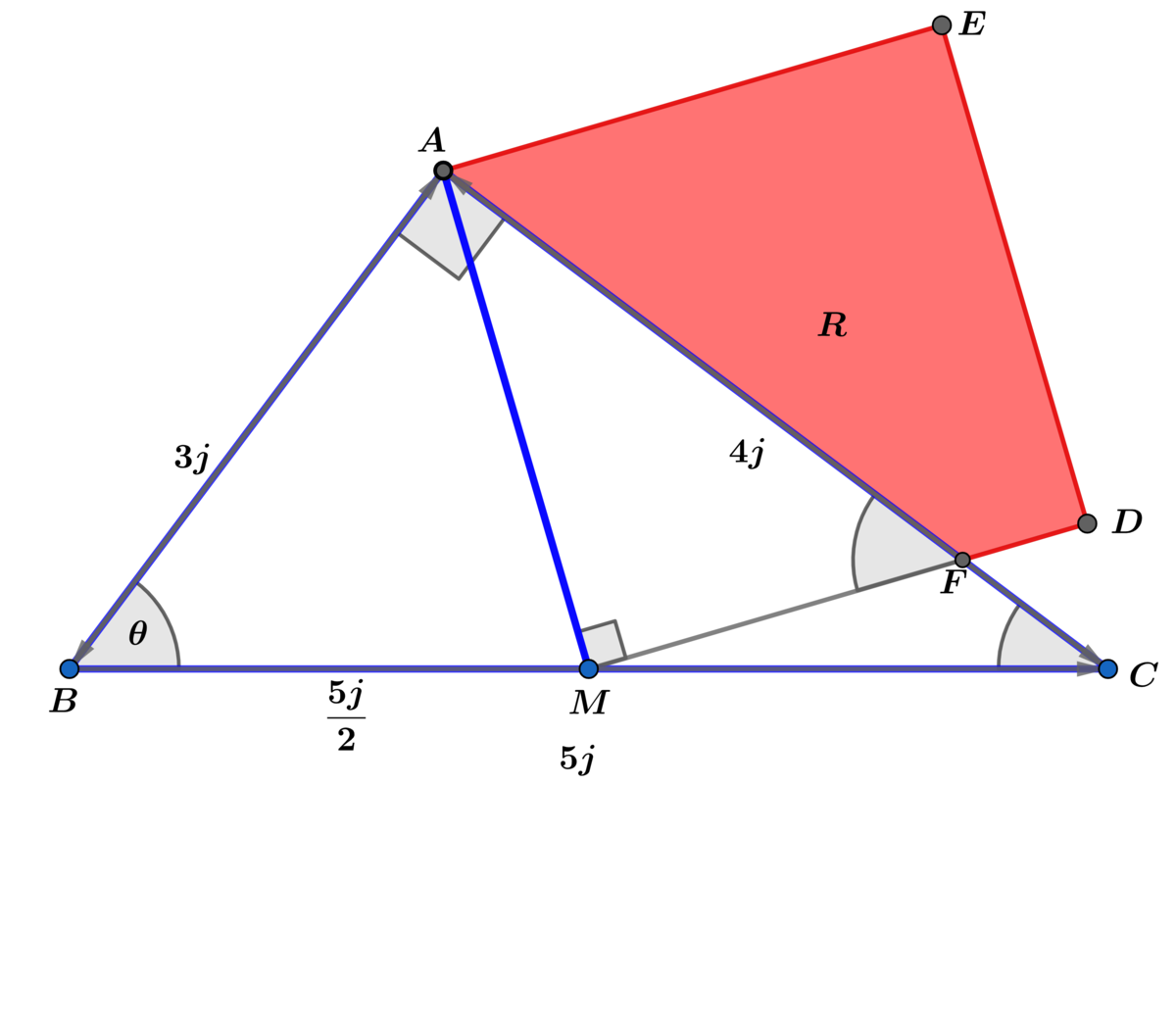
( 3 j , 4 j , 5 j ) is a Pythagorean triple ⟹ △ A B C is a right triangle with m ∠ A = 9 0 ∘ and cos ( θ ) = 5 3
Using the law of cosines on △ B A M with included ∠ A B C = θ ⟹
A M 2 = 9 j 2 + 4 2 5 j 2 − 2 ( 3 j ) ( 2 5 j ) ( 5 3 ) = 4 2 5 j 2 ⟹ A M = 2 5 j ⟹
M F = A F cos ( θ ) = 5 3 A F ⟹
A F 2 = 4 2 5 j 2 + 2 5 9 A F 2 ⟹ 2 5 1 6 A F 2 = 4 2 5 j 2 ⟹ A F = 8 2 5 j
⟹ M F = 5 3 ( 8 2 5 ) j = 8 1 5 j ⟹ A △ A M F = 2 1 ( 2 5 j ) ( 8 1 5 j ) = 3 2 7 5 j
⟹ A R = A A E D F = 4 2 5 j 2 − 3 2 7 5 j 2 = 3 2 1 2 5 j 2 = 2 5 0 ⟹ j 2 = 6 4 ⟹ j = 8 .
Since ( 3 j ) 2 + ( 4 j ) 2 = ( 5 j ) 2 , △ A B C is a right triangle, and by Thales's Theorem right ∠ A will lie on the circle that has B C as its diameter.
Since M is the midpoint of B C , M is the center of that circle, and M B = M A = M C = 2 5 j , so △ A C M is an isosceles triangle.
As two base angles of an isosceles triangle, ∠ M C A = ∠ M A C , which means △ A M F ∼ △ C A B by AA similarity.
Since △ A M F ∼ △ C A B , M F = M A ⋅ A C A B = 2 5 j ⋅ 4 j 3 j = 8 1 5 j .
Then A A E D F = A M A E D − A △ A M F = ( 2 5 j ) 2 − 2 1 ⋅ 8 1 5 j ⋅ 2 5 j = 3 2 1 2 5 j 2 = 2 5 0 , which solves to j = 8 .