Triples Relationship
x = y z y = x z z = x y
Let the triples ( x , y , z ) of non-zero real numbers. How many ordered triplets ( x , y , z ) satisfy the system of equations above?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Bonus question : Can you generalize this? That is, If a 1 , a 2 , … , a n are non-zero numbers such that any a i is the product the other a i 's. What is the ordered solutions for ( a 1 , a 2 , … , a n ) for n ≥ 3 ? In this case, n = 3 yield 4 solutions.
(Updated)
Now it is allright
Moderator note:
You made a few careless mistakes.
There's a much simpler approach.
Hint : Multiply them all together.
The last 2 answers are incorrect since they do not meet the 3 relations coz we get 1×1 which is never equal to -1. So first 2 answers are correct but the last 2 answers needs to be seen through.
Log in to reply
yeah u're right i just made a mistake
the triples are ( 1 , 1 , 1 ) ; ( − 1 , 1 , − 1 ) , ( − 1 , − 1 , 1 ) ; ( 1 , − 1 , − 1 )
sorry for the mistake , thank you for your observation
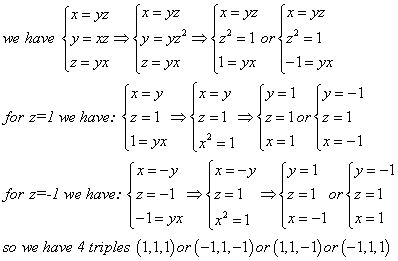
x y z = ( x y z ) 2 ⟹ x y z = 1 or 0
But we need to find non zero solutions ⟹ ( x , y , z ) = ( 1 , 1 , 1 ) , ( − 1 , − 1 , 1 ) , ( 1 , − 1 , − 1 ) , ( − 1 , 1 , − 1 )
So answer is 4