Triplication
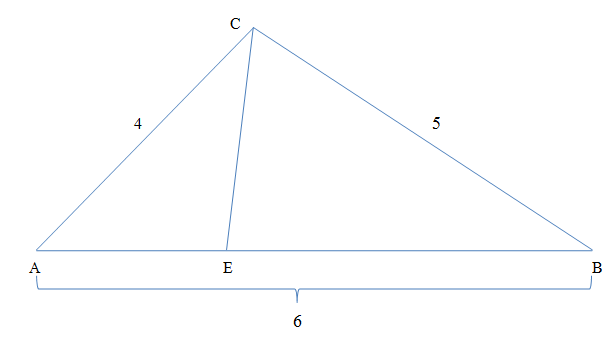
In △ A B C , A C = 4 , B C = 5 , and A B = 6 , point E is on A B so that A E = 2 1 E B .
If the sums of C E and the measure of the segment from E to the midpoint of C B can be written as: 2 1 P + Q R , where P , Q , R are all integers. Find P .
The answer is 73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Basically same as Mr. Guilherme Niedu and MR. Marta Reece but little different.
A
E
=
2
,
a
n
d
E
B
=
4
,
l
e
t
∠
C
A
B
=
∠
C
A
E
=
α
,
a
n
d
M
m
d
p
o
i
n
t
o
f
C
B
.
U
s
i
n
g
C
o
s
R
u
l
e
i
n
Δ
s
,
C
A
B
a
n
d
C
A
E
,
C
o
s
α
=
2
∗
4
∗
6
4
2
+
6
2
−
5
2
=
9
.
A
l
s
o
C
o
s
α
=
2
∗
4
∗
2
4
2
+
2
2
−
C
E
2
=
2
0
−
C
E
2
.
∴
C
E
=
1
1
.
I
n
Δ
C
E
B
,
m
e
d
i
a
n
E
M
=
2
1
∗
2
1
∗
(
C
E
2
+
6
2
−
5
2
)
=
2
1
2
9
.
∴
C
E
+
E
M
=
2
1
4
4
+
2
1
2
9
=
2
1
4
4
+
2
9
+
Q
R
⟹
P
=
7
3
.
.
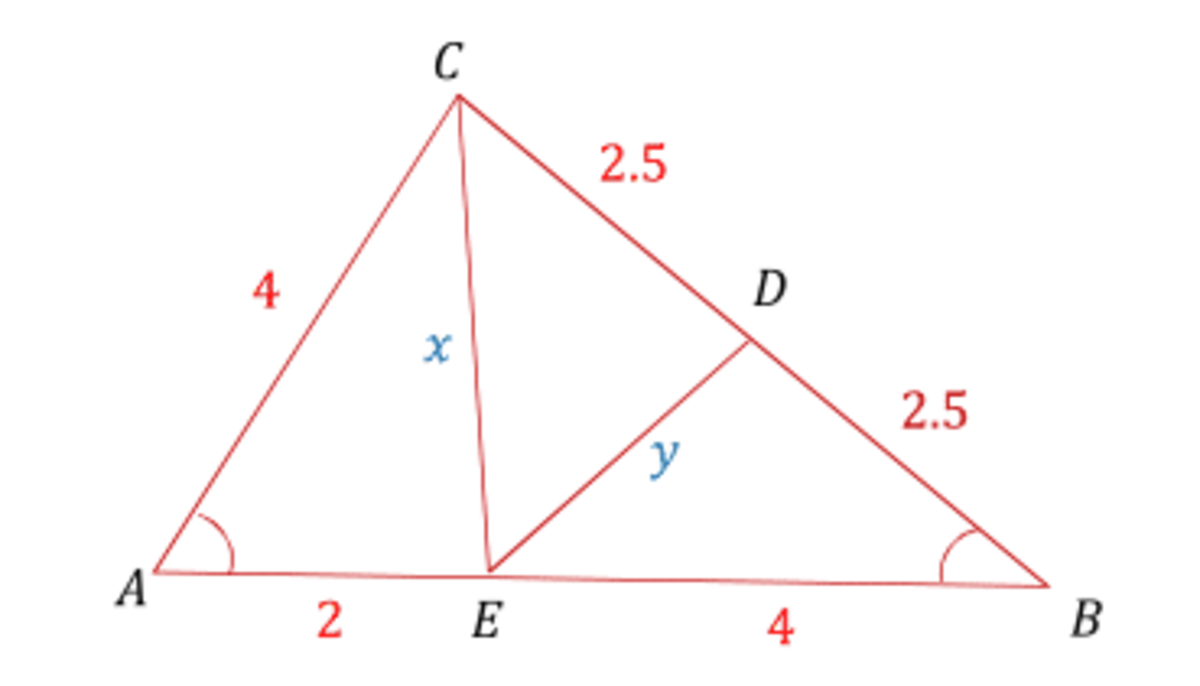 From
△
A
B
C
we get
c
o
s
(
C
A
B
)
=
2
×
4
×
6
4
2
+
6
2
−
5
2
=
1
6
9
From
△
A
B
C
we get
c
o
s
(
C
A
B
)
=
2
×
4
×
6
4
2
+
6
2
−
5
2
=
1
6
9
From △ A E C and again the law of cosines x = 4 2 + 2 2 − 2 × 2 × 4 × c o s ( C A B ) = 1 1
Again from △ A B C comes c o s ( A B C ) = 2 × 5 × 6 5 2 + 6 2 − 4 2 = 4 3
And from △ D E B we calculate y = 2 . 5 2 + 4 2 − 2 × 2 . 5 × 4 × c o s ( A B C ) = 2 2 9
So x + y = 1 1 + 2 2 9 .
This is a perfectly good answer. It does not, however, fit the required format. To do that, we have to show what it is a squire root of, in other words square it and put that under a square root. With a little simplification, that becomes.
x + y = 2 1 7 3 + 4 3 1 9 .
We can directly apply Stewart's theorem.
Log in to reply
and appolonius theorem which is the special case of it.
Let us define as F the midpoint of B C . A E = 2 , B E = 4 , B F = C F = 2 . 5 . By cosine law:
B C 2 = A C 2 + A B 2 − 2 ⋅ A C ⋅ A B c o s ( A ^ )
2 5 = 1 6 + 3 6 − 4 8 c o s ( A ^ )
c o s ( A ^ ) = 1 6 9
A C 2 = A B 2 + B C 2 − 2 ⋅ A B ⋅ B C c o s ( B ^ )
1 6 = 2 5 + 3 6 − 6 0 c o s ( B ^ )
c o s ( B ^ ) = 4 3
C E 2 = A C 2 + A E 2 − 2 ⋅ A C ⋅ A E c o s ( A ^ )
C E 2 = 1 6 + 4 − 9
C E = 1 1
E F 2 = B E 2 + B F 2 − 2 ⋅ B E ⋅ B F c o s ( B ^ )
E F 2 = 4 2 5 + 1 6 − 1 5
E F = 2 2 9
C E + E F = 1 1 + 2 2 9
C E + E F = ( 1 1 + 2 2 9 ) 2
C E + E F = 1 1 + 4 2 9 + 3 1 9
C E + E F = 2 1 7 3 + 4 3 1 9
A = 7 3 , B = 4 , C = 3 1 9