Tripod Moment

Classical Mechanics Level 2

A tripod is made of wire with a linear mass density of 1 1 . The tripod consists of four parts:

1) A circular base of radius 1 1 , contained within the x y xy plane, with its center at the origin
2) A straight line segment from ( 1 , 0 , 0 ) (1,0,0) to ( 0 , 0 , H ) (0,0,H)
3) A straight line segment from ( − 1 2 , 3 2 , 0 ) \Big ( -\frac{1}{2}, \frac{\sqrt{3}}{2}, 0 \Big ) to ( 0 , 0 , H ) (0,0,H)
4) A straight line segment from ( − 1 2 , − 3 2 , 0 ) \Big ( -\frac{1}{2}, -\frac{\sqrt{3}}{2}, 0 \Big ) to ( 0 , 0 , H ) (0,0,H)

The attached image shows the projection onto the x y xy plane (to-scale), and the projection onto the y z yz plane (not to-scale).

If the moment of inertia of the entire tripod with respect to the z z axis is 1.5 1.5 times as large as that of the circular base alone, what is the tripod height H H ?


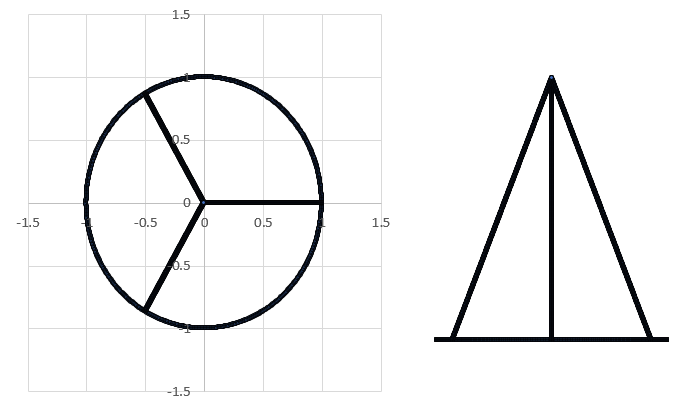
The answer is 2.9782.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Moment of inertia of each straight segment about the z-axis is (√(1+H^2))/3, and of the circle is 2π. Therefore by the given condition of the problem, π=√(1+H^2), or H=√(π^2-1)=2.9781881070694

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...