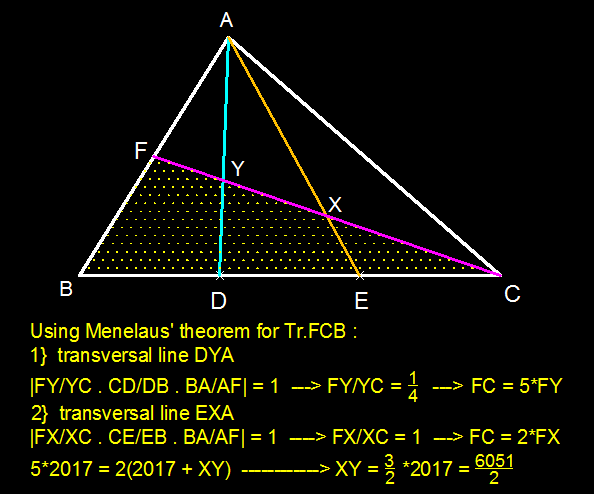
Trisect a Median

The position of point $A$ is immaterial because ratios between segments in the same direction are not affected by affine transformations. We choose affine coordinates with $B$ at the origin, $BC$ along the $x$ -axis, and $BA$ along the $y$ -axis, and choose units such that $BC_1 = BA_1 = 10$ .

The coordinates of relevant points are now $C_1:\ (0,10)$ ; $A_1:\ (10,0)$ ; $A_2:\ (20,0)$ . The equations for the various lines of interest are $\ell_0 (C_1C):\ y = 10-\tfrac13 x, \\ \ell_1 (A_1A):\ y = 20 - 2x, \\ \ell_2 (A_1A):\ y = 20 - x.$ Equating $\ell_0$ and $\ell_1$ gives $Y:\ (6, 8)$ ; likewise, equating $\ell_0$ and $\ell_2$ gives $X:\ (15, 5)$ .

Now the segment $C_1Y$ is given by the vector $(6,-2)$ , and the segment $YX$ by the vector $(9, -3)$ . Clearly $\frac{YX}{C_1Y} = \frac 3 2,$ so that $YX = \frac 3 2 \cdot 2017 = \frac{6051}{2}.$ We submit the result $6051 + 2 = \boxed{6053}$ .

For this solution, we will apply the Ratio Lemma, which states that for any point $X'$ on side $YZ$ of triangle $XYZ$ , we have

$\dfrac{XY}{XZ} \cdot \dfrac{\sin \angle YXX'}{\sin \angle X'XZ} = \dfrac{YX'}{X'Z}.$

First, we will find $\dfrac{AX}{AA_2}$ . Let $\alpha_1 = \angle ACC_1$ and $\alpha_2 = \angle C_1CB$ . By the lemma, we know that $\dfrac{AC_1}{C_1B} = \dfrac{AC}{BC} \cdot \dfrac{\sin \alpha_1}{\sin \alpha_2}.$ Thus, $\dfrac{AC}{BC} \cdot \dfrac{\sin \alpha_1}{\sin \alpha_2} = 1.$ We also can find that $\dfrac{AX}{XA_2} = \dfrac{AC}{CA_2} \cdot \dfrac{\sin \alpha_1}{\sin \alpha_2}.$ Using the equation we derived and the fact that $A_2C = \dfrac{BC}{3}$ , we get $\dfrac{AX}{XA_2} = 3,$ which indicates that $\dfrac{AX}{AA_2} = \dfrac{3}{4}$ .

Now, we apply the same strategy we used to find $\dfrac{AX}{AA_2}$ to find $\dfrac{C_1Y}{YX}$ . Let $\beta_1 = \angle BAA_1$ and $\beta_2 = \angle A_1AA_2$ . By the Ratio Lemma, we can find that $\dfrac{AB}{AA_2} \cdot \dfrac{\sin \beta_1}{\sin \beta_2} = \dfrac{BA_1}{A_1A_2} = 1$ and $\dfrac{C_1Y}{YX} = \dfrac{AC_1}{AX} \cdot \dfrac{\sin \beta_1}{\sin \beta_2}.$ Plugging in $C_1A = \dfrac{AB}{2}$ and $AX = \dfrac{3AA_2}{4}$ into the latter equation, we can simplify it into $\dfrac{C_1Y}{YX} = \dfrac{2}{3}.$ Setting $C_1Y = 2017$ and solving for $XY$ yields $XY = \dfrac{6051}{2}$ . Thus, $p + q = \boxed{6053}$ .

Draw a line segment through $C_1$ parallel to side $BC$ .

$\angle YCA_1 = \angle XCA_2 = \angle YC_1Y_1 = \angle XC_1X_1$ (Alternate angles)

$\angle C_1YY_1 = \angle CYA_1$ and $\angle C_1XX_1 = \angle CXA_2$ (Vertically Opposite Angles)

Therefore, $\triangle YA_1C \sim \triangle YY_1C_1$

Since $C_1B_1$ is parallel to side $BC$ and $C_1$ is the midpoint of side $AB$ .

$\displaystyle\frac{AC_1}{AB} = \frac{C_1Y_1}{BA_1} = \frac{Y_1X_1}{A_1A_2} = \frac{X_1B_1}{A_2C} = \frac{1}{2}$ (Basic proportionality theorem)

Therefore, $Y_1$ and $X_1$ trisect $C_1B_1$ .

Let $BA_1 = A_1A_2 = A_2C = 2x$ then

$C_1Y_1 = Y_1X_! = X_1B_1 =x$

Therefore, $\displaystyle\frac{A_1C}{Y_1C_1} = \frac{4x}{x} = 4$

Since $\triangle YA_1C \sim \triangle YY_1C_1$

$\displaystyle\frac{CY}{C_1Y} = \frac{A_1C}{Y_1C_1} = \frac{4x}{x} = 4$

$\displaystyle\frac{C_1X_1}{CA_2} = \frac{C_1Y_1 + Y_1X_1}{CA_2} = \frac{x+x}{2x} = 1$

Therefore, $\triangle C_1XX_1 \cong \triangle CXA_2$

Therefore, $C_1X = CX$

$\displaystyle\frac{CY}{C_1Y} = \frac{YX+CX}{C_1Y} = 4$

But $C_1X = CX$

$\displaystyle\frac{YX+C_1X}{C_1Y} = 4$

$\displaystyle\frac{YX+C_1Y +YX}{C_1Y} = 4$

$\displaystyle\frac{2YX+C_1Y}{C_1Y} = 4$

$\displaystyle YX = \frac{3C_1Y}{2}$

$\displaystyle YX = \frac{3 \times 2017}{2}$

$\displaystyle YX = \frac{6051}{2}$

Therefore, Ans is $6051 + 2 = 6053$

This is a sort of a brute force method of solving the problem since I was too lazy to use trigonometry and I couldn't think of a simpler geometric method. Since no angle is given in this problem, I assumed that this is a constant value for all triangles. To simplify the problem, I used an equilateral triangle so that the side lengths of the triangle would be equal. I plotted this in the cartesian plane with a side length of 1. I graphed the median through point C and found the function to be $y=-\frac{\sqrt{3}}{3}x+\frac{\sqrt{3}}{3}$ . I then found the equation of the lines for the trisectors of line BC $AA_1$ and $AA_2$ , which turned out to be $y=3\sqrt{3}x-\sqrt{3}$ and $y=-3\sqrt{3}x+2\sqrt{3}$ respectively. Solving for x and substituting for y, I got point Y is $(\frac{2}{5},\frac{\sqrt{3}}{5})$ and point X is $(\frac{5}{8}, \frac{\sqrt{3}}{8})$ . Using pythagorean theorem, I found that $C_{1}Y = \frac{\sqrt{3}}{10}$ and $YX = \frac{6\sqrt{3}}{40}$ . From there, I found $\frac{YX}{C_{1}Y} = \frac{\frac{6\sqrt{3}}{40}}{\frac{\sqrt{3}}{10}} = \frac{60}{40} = \frac{3}{2}$ So in the diagram, $YX = \frac{3}{2} \cdot 2017 = \frac{6051}{2}$ Adding $6051$ and $2$ gets us $6051+2 = \boxed{6053}$

This is not the nicest solution but areal coordinates do work quite well:

Using areal coordinates with respect to triangle ABC, the coordinates of the points are:

$A = (1, 0, 0)\\ B = (0, 1, 0)\\ C = (0, 0, 1)\\ A_1 = (0, \frac{2}{3}, \frac{1}{3})\\ A_2 = (0, \frac{1}{3}, \frac{2}{3})\\ C_1= (\frac{1}{2}, \frac{1}{2}, 0)\\$

The equation of the line $AA_1$ is $y=2z$ and the equation of the line $AA_2$ is $y=\frac{1}{2} z$

The equation of the line $CC_1$ is $x=y$

Solving simultaneously gives $Y = (\frac{2}{5}, \frac{2}{5}, \frac{1}{5})$ and $Z= (\frac{1}{4}, \frac{1}{4}, \frac{1}{2})$

The displacement vector $C_1Y$ is $(\frac{1}{10}, \frac{1}{10}, -\frac{1}{5})$ . Using the distance formula, $(C_1Y)^2 = \frac{1}{50} a^2 + \frac{1}{50}b^2 - \frac{1}{100}c^2 = 2017^2$

Similarly, the distance $(YX)^2 = \frac{9}{200} a^2 + \frac{9}{200} b^2 - \frac{9}{400} c^2 \\= \frac{9}{4} ( \frac{1}{50} a^2 + \frac{1}{50}b^2 - \frac{1}{100}c^2) \\= \frac{9}{4} × 2017^2$

So $XY = \sqrt(\frac{9(2017^2)}{4}) = \frac{6051}{2}$ . The answer is therefore $6051+2 = \boxed{6053}$