Trisected Area?
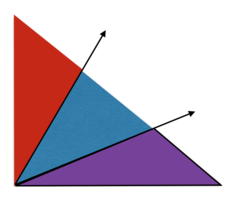
Does trisecting the 9 0 ∘ angle in a non-degenerate right triangle create 3 triangles of equal area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
I love thinking about the circle case first, and how this differs unfavorably. Thanks for sharing, and the simulation is awesome too!
However, I think you should make the first part more rigorous by showing why cutting through this region cannot achieve the equality that the curved region does. It seems "obvious", but you haven't explicitly shown it.
(please excuse the diagram quality)

Suppose all 3 areas are equal. The area of any triangle is 2 a b sin C . But the red and blue triangle share a side and the same angle C = 3 0 ∘ , so their other sides (from the two trisecting segments) must be equal; similarly for the blue and purple triangles.
Then, via isosclees triangles, we have the angles A , B shown. But this means that A + B = 9 0 ∘ (from the right triangle) but A + B = 1 8 0 ∘ − 3 0 ∘ = 1 5 0 ∘ (from the blue triangle), so this is impossible.
i did it the same way!
brilliant!
More generally, trisecting an angle in any triangle never leads to three equal areas.
Suppose we trisect angle A in triangle A B C , and we obtain three triangles of equal area. Let the trisecting lines meet B C at H and I , so that H is between C and I .
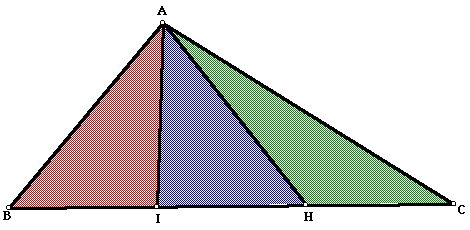 http://jwilson.coe.uga.edu/emt668/EMAT6680.2000/Lehman/emat6690/image5.gif
http://jwilson.coe.uga.edu/emt668/EMAT6680.2000/Lehman/emat6690/image5.gif
Let θ = ∠ B A I = ∠ I A H = ∠ H A C . Triangles A B I and A I H have equal area, so 2 1 A B ⋅ A I sin θ = 2 1 A I ⋅ A H sin θ , which simplifies to A B = A H . Then by SAS, triangles A B I and A H I are congruent. It follows that ∠ A I B = ∠ A I H , so ∠ A I B = ∠ A I H = 9 0 ∘ . In other words, A I is perpendicular to B C . By the same reasoning on triangles A I H and A H C , A H is also perpendicular to B C , contradiction.
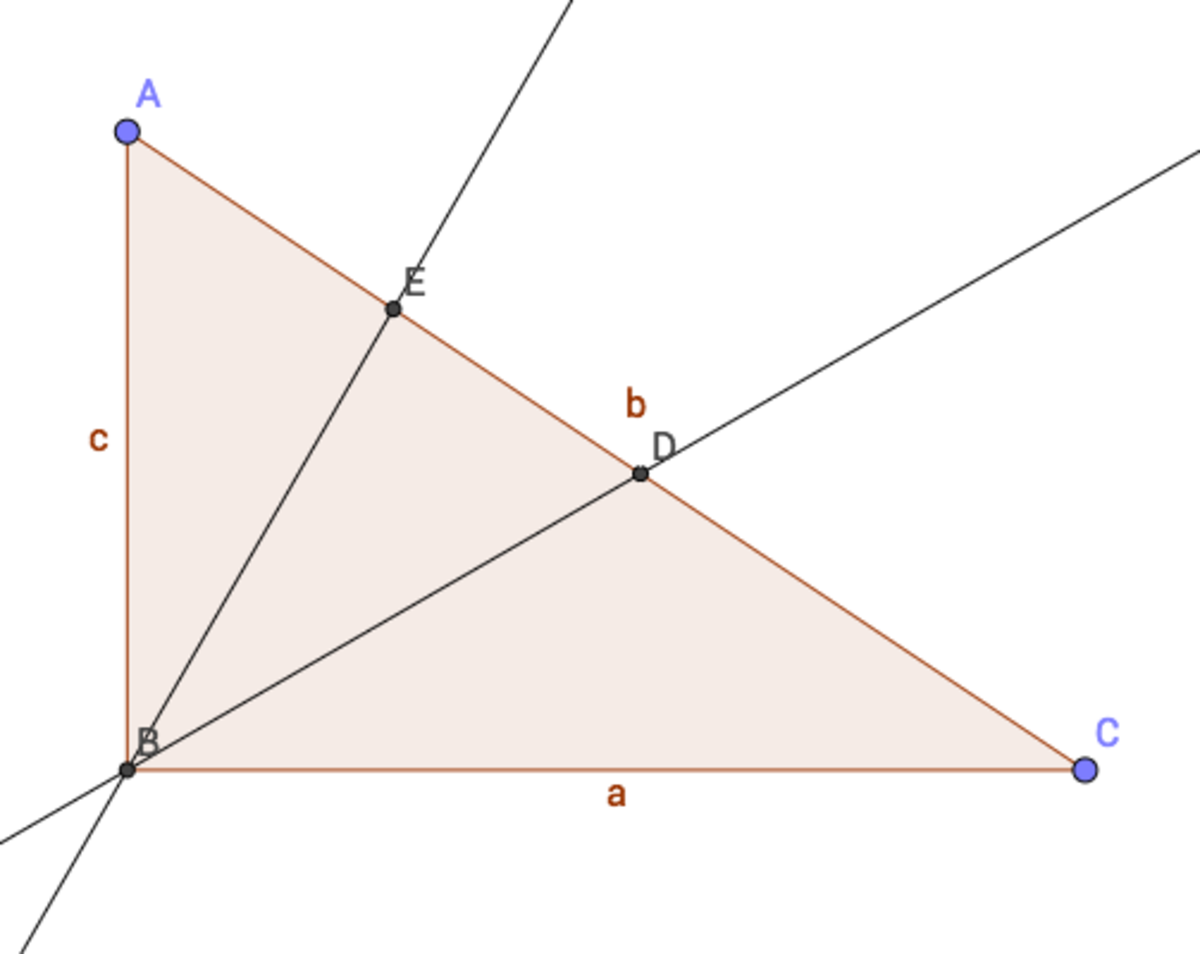
Simple proof using angle bisector theorem and areas of triangles. Assume there does exist some right angle triangle which satisfies.
Thus, since ∣ A B E ∣ = ∣ D B E ∣ , and they share the same altitude from B , A E = E D . We also have ∠ A B E = ∠ E B D , so by angle bisector theorem, B D A B = D E A E = 1 , so A B = B D . Similarly, B E = B C .
We have ∠ B A D = ∠ B D E , and 9 0 ∘ − ∠ B A D = ∠ B C E = ∠ B E D . Thus, ∠ E B D = 1 8 0 ∘ − ( ∠ B D E + ∠ B E D ) = 1 8 0 ∘ − 9 0 ∘ = 9 0 ∘ . But we already have 3 ∠ E B D = ∠ A B C , so ∠ A B C = 2 7 0 ∘ = 9 0 ∘ . This is a contradiction so there must not exist a triangle which satisfies.
Do you mean B D A B = E D A E = 1 ?
SOLVED it the same way. Nice observation, the other solutions make use of trigonometry , radians.
Area of triangle =1/2 sinb a c Using this formula. Since Sina is same for all three triangles, sides also need to be same length for equal area. This becomes impossible
By inspection, if the hypotenuse of the overall (combined) triangle is considerably steeper than 45 degrees then clearly the upper red triangle is larger than the lower purple one. And vice-versa if the hypotenuse is considerably shallower than 45 degrees. Thus we know that at least in some cases the three triangular areas are not equal. To determine whether they are NEVER equal, we need to focus on the situation where the hypotenuse is exactly 45 degrees. If in that case all three sub-triangles are equal, then the answer would be “depends on the triangle”; otherwise the answer would be “no, never”. In the 45-degree case, inspection again indicates that the upper and lower triangles are equal in area. But what about the middle one? Some simple calculations show that the ratio of the area of the entire (combined) triangle to the area of the lower triangle is 1 : 1/(1 + sqrt(3)). Now, 1/(1 + sqrt(3)) is a bit less than 1/3. This means that in the special case of a 45-degree hypotenuse, the lower (and also the upper) triangle is slightly less than 1/3 of the overall area. Hence in that special case the three triangles are not equal either. So, the answer is “no, never”.
For any triangle that has one of its angles trisected, if all the areas so formed have equal areas, then because they all share the same altitude, the side opposite of the trisected angle is also therefore trisected. Then that suggests that a triangle can have an angle bisector that also bisects the side opposite of the bisected angle, as per this graphic
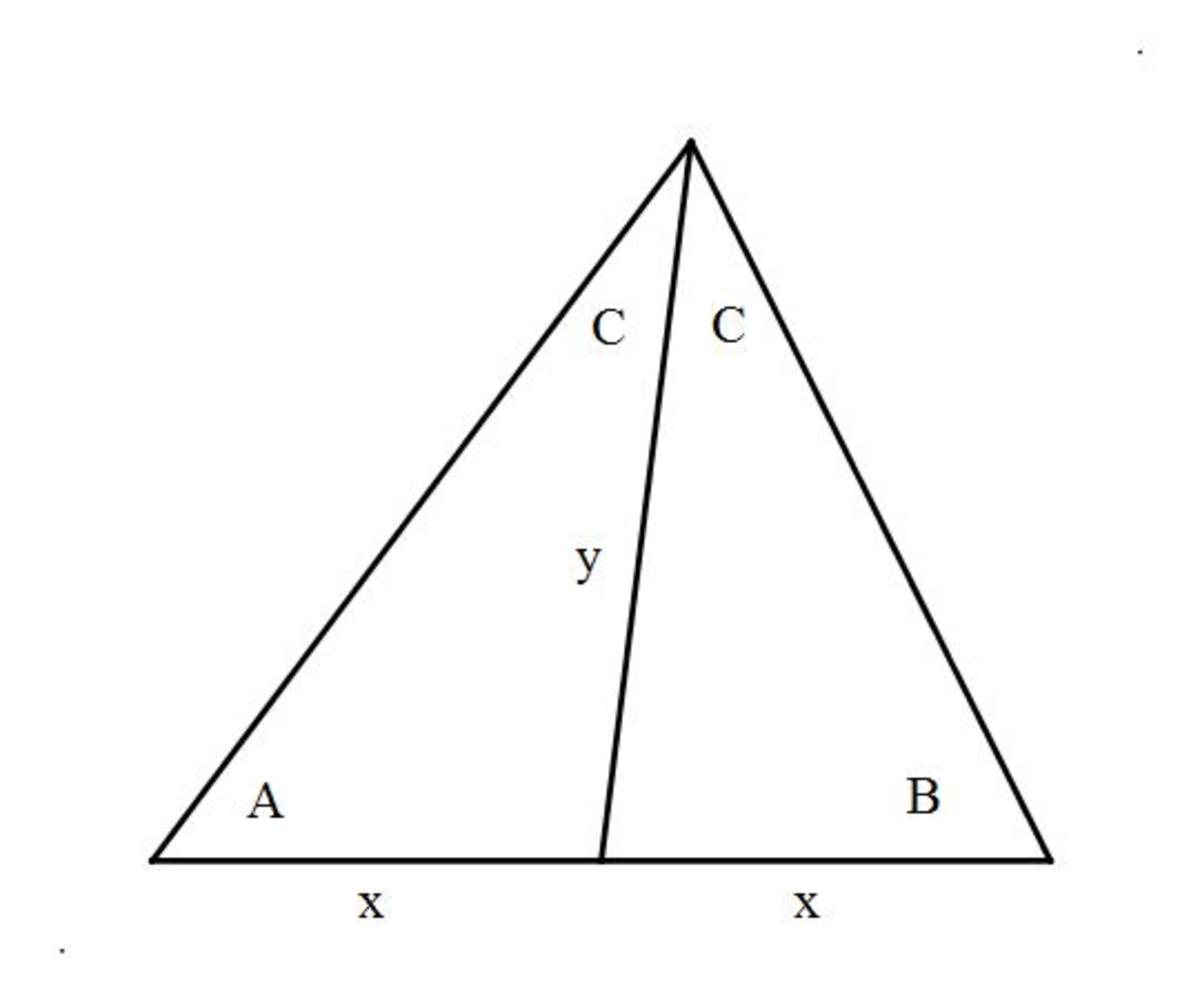
But, by using the Sine Law, that means, or leads to S i n ( A ) = S i n ( B ) which is only possible if the triangle is isosceles, leading to the conclusion that the middle of the trisected areas is an isosceles with both base angles that are right angles.
This is similar to Jon Haussman's proof already given here.
Before answering the question, it would be helpful to understand the relationship between the radius and area of trisected regions. It's interesting to show the circle case first before I show some proof.
Geometric Analysis of the Circle
Consider the following diagram of the unit quarter circle whose trisection (dividing into 3 congruent angles of measure 3 0 ∘ ) takes place at its center: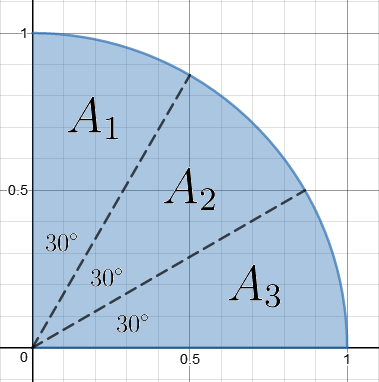 Figure 1. Shaded region of quarter circle.
Clearly, trisecting the unit quarter circle divides into 3 regions of equal area
A
=
1
2
π
Extending this case to a circle of any arbitrary radius
r
, we see that the area of the trisected region is
A
r
=
1
2
π
r
2
As long as the line formed by two points (each along the straight line) is the
circular arc
(or the shape is a symmetrical right-angle polygon of
3
k
+
2
sides for positive integer
k
; see Figure 2), this guarantees 3 regions of equal areas, such that
A
quarter circle
=
3
A
r
=
4
π
r
2
Figure 1. Shaded region of quarter circle.
Clearly, trisecting the unit quarter circle divides into 3 regions of equal area
A
=
1
2
π
Extending this case to a circle of any arbitrary radius
r
, we see that the area of the trisected region is
A
r
=
1
2
π
r
2
As long as the line formed by two points (each along the straight line) is the
circular arc
(or the shape is a symmetrical right-angle polygon of
3
k
+
2
sides for positive integer
k
; see Figure 2), this guarantees 3 regions of equal areas, such that
A
quarter circle
=
3
A
r
=
4
π
r
2
Mini Proof
If suppose we have the smaller quarter circle with radius r s , such that 0 < r s < r where r is the large radius, then A s = 4 π ( r s ) 2 Cutting in a perfect circular line of the large circle gives A outer = 4 π ( r 2 − ( r s ) 2 ) which shows that the area of each trisected outer region is A \substack outer trisected = 1 2 π ( r 2 − ( r s ) 2 ) This can also be verified by evaluating and combining the areas of both inner and outer trisected regions to show we can achieve the area of the large quarter circle.
Answering the Question
As we already know, 3 congruent regions work if we are to trisect the circular region. Since a right triangle is clearly not circular, there is no way to obtain 3 congruent areas. For those who want to explicitly know why this doesn't work for right triangles, here is the proof by contradiction:
Suppose all three regions of the right triangle have the same area. Consider another illustration: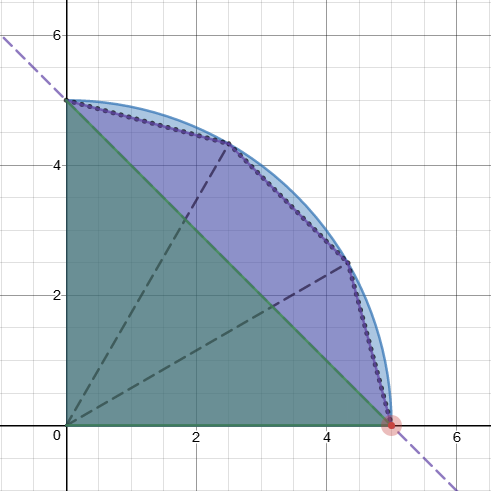 Figure 2. Combined shaded regions of different colors. Green region resembles right triangle, whereas purple triangular regions resembles the sliced trisected regions
Since all 3 original blue arc regions has the same area, each of the 3 purple regions (formed by the chords) have the same area as each other. However, since it takes at least 3 cuts to form such regions, it is impossible to make 1 straight cut.
Figure 2. Combined shaded regions of different colors. Green region resembles right triangle, whereas purple triangular regions resembles the sliced trisected regions
Since all 3 original blue arc regions has the same area, each of the 3 purple regions (formed by the chords) have the same area as each other. However, since it takes at least 3 cuts to form such regions, it is impossible to make 1 straight cut.
Note 1: Another way to look at this diagram is to slice through the purple region with the straight line and note that there is no way to achieve remaining trisected purple regions of equivalent areas. This also disproves that the trisected areas of the triangle can't be the same.
Note 2: It is possible to have at most two congruent trisected regions (with only one cut from one point to another as shown in Figure 2) if the whole right triangle is either 3 0 - 6 0 - 9 0 or 4 5 - 4 5 - 9 0 , which is left for the readers to work out.
Here is the fun simulation , which I print-screened to illustrate the solution. The graph is done by Desmos. Hope you have fun with it!