Trisected Triangle
In acute triangle A B C , O is an interior point. The perpendiculars from O to sides B C , C A and A B intersect the respective sides at D , E and F . Given that F A = 1 2 , A E = 8 , E C = 1 3 , C D = 1 1 , D B = 1 4 , what is the length of B F ?
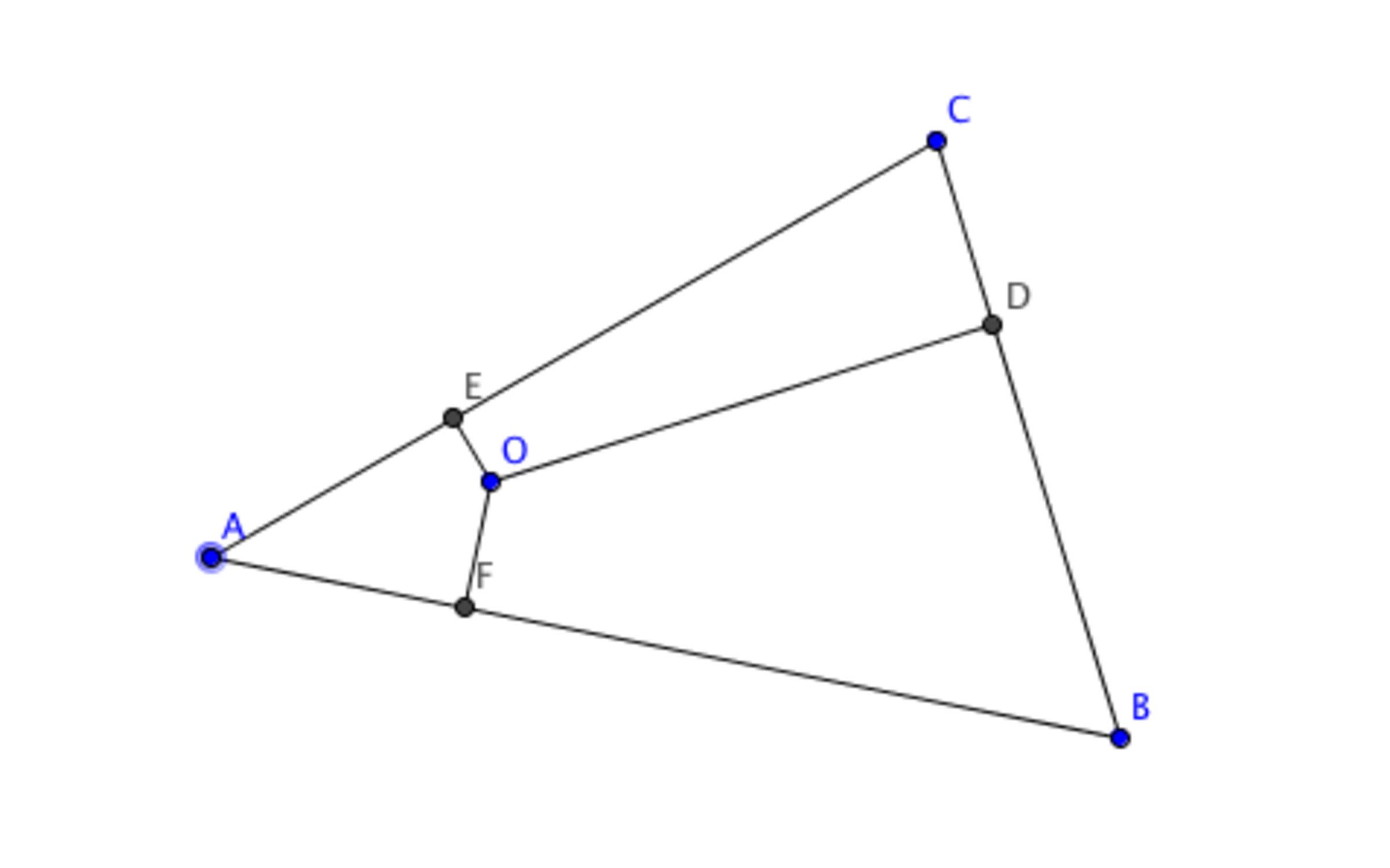
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Same MEthod!! Upvoted
Applying Pythagorean theorem,
Δ
s
A
E
O
a
n
d
A
F
O
,
E
O
2
+
8
2
=
A
O
2
=
F
O
2
+
1
2
2
.
Δ
s
C
D
O
a
n
d
C
E
O
,
D
O
2
+
1
1
2
=
C
O
2
=
E
O
2
+
1
3
2
.
Δ
s
B
F
O
a
n
d
B
D
O
,
F
O
2
+
F
B
2
=
D
O
2
=
F
O
2
+
1
4
2
.
Adding the first & last terms of the three equations, and canceling same terms of both sides,
8
2
+
1
1
2
+
F
B
2
=
1
2
2
+
1
3
2
+
1
4
2
.
⟹
F
B
=
1
2
2
+
1
3
2
+
1
4
2
−
8
2
−
1
1
2
.
=
1
8
.
Applying Pythagorean theorem, we get that A F 2 + C E 2 + B D 2 = O A 2 − O F 2 + O C 2 − O E 2 + O B 2 − O D 2 and A E 2 + C D 2 + B F 2 = O A 2 − O E 2 + O C 2 − O D 2 + O B 2 − O F 2 , hence these values are equal to each other.
Thus B F 2 = 1 2 2 + 1 3 2 + 1 4 2 − 1 1 2 − 8 2 so B F = 1 8 .