Trisectors in a triangle

First we are going to introduce a formula for the length of the bisector of a triangle in terms of the two sides forming the corresponding angle and the cosine of the half of the same angle.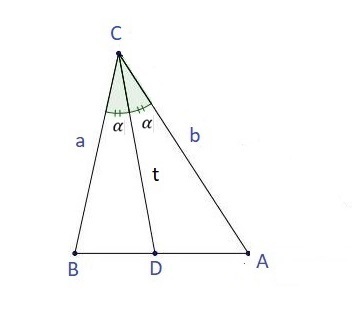

Since the area of the triangle $ABC$ is the sum of the areas of the two triangles $BCD$ and $ACD,$ then we have that $\frac{1}{2}at\sin \alpha +\frac{1}{2}tb\sin \alpha = \frac{1}{2}ab\sin 2\alpha .$ Then using that $\sin 2\alpha=2 \sin \alpha \cos \alpha$ and solving for $t,$ we get that $t=\frac{2ab\cos \alpha}{a+b}.$ We can use this formula to express the $x$ and $y,$ using the triangles $ACD$ and $BCE,$ respectively (look at the figure below).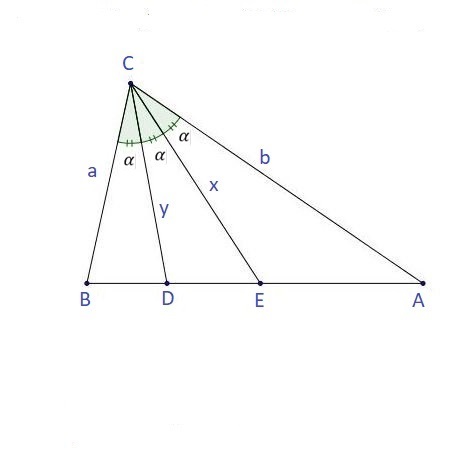 So we get the following $y=\frac{2ax\cos \alpha}{a+x} \:\: \text{and}\:\:x= \frac{2by\cos \alpha}{b+y}.$ Now, replacing in both equations the $y$ by $\frac{2}{3}x,$ we obtain the equations $\frac{2}{3}x=\frac{2ax\cos \alpha}{a+x} \:\: \text{and}\:\:x= \frac{2b(\frac{2}{3}x)\cos \alpha}{b+\frac{2}{3}x}.$

Solving both equations for $\cos\alpha,$ we get that $\cos\alpha=\frac{a+x}{3a}\:\: \text{and}\:\: \cos\alpha=\frac{3b+2x}{4b}.\:\:\:\:(*)$ Making the two expressions equal and solving for $x$ we get that $x=\frac{5ab}{4b-6a}.$ Substituting the $x$ by this expression in one of the equations of $(*),$ we obtain that $\cos\alpha=\frac{3b-2a}{4b-6a}.$

Of course, it is clear that $\alpha$ is an acute angle, and then $0<\frac{3b-2a}{4b-6a}<1.$ Since $a<b,$ then $3b-2a>0,$ and, therefore, $4b-6a >0,$ because, otherwise, $\frac{3b-2a}{4b-6a}$ would not be positive. That is, the numerator and the denominator of the fraction $\frac{3b-2a}{4b-6a}$ are both positive. Now, we can see that if assume that $0<\frac{3b-2a}{4b-6a}\leq\frac{3}{4},$ then we obtain that $10a\leq 0$ that is a contradiction. Assuming that $\frac{3}{4}<\frac{3b-2a}{4b-6a}<1,$ and solving both inequalities for $\frac{a}{b},$ we obtain that $0<\frac{a}{b}$ and $\frac{a}{b}<\frac{1}{4},$ respectively. The first of these two inequalities is always true, and the second tells us that the minimum value of $k$ is less than or equal to $\frac{1}{4}.$ Now we should prove that $\frac{1}{4}$ is equal to the smallest value of $k$ . Let us make $s= \frac{3b-2a}{4b-6a}$ . It is clear that $s$ can made as close to 1 from below as you want. It is easy to get that $\frac{a}{b}=\frac{4s-3}{6s-2}$ that tends to $\frac{1}{4}$ as $s \rightarrow 1^-$ . This proves that $\frac{1}{4}$ is the smallest number $k$ for which the inequality $\frac{a}{b}<k$ is always true for all possible values of $a$ and $b.$ Therefore, the answer for the question is $\boxed{0.25}$