Trisectors!
Let A B C D be a square. Points E , F , G , H are on the line segments A B , B C , C D , D A respectively such that 2 A E = E B , 2 B F = F C , 2 C G = G D , and 2 D H = H A . The area bounded by the line segments A G , B H , C E , D F is a square with side length 1. If A B can be written as a b , where a and b are positive integers such that b is square-free, find a + b .
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Pay attention with the equalities 2AE = BE etc... You can also obtain a result of 6 if you bild E outside of the square like symetric of B regarding A etc... Vert nice problem except this little point
@Sharky Kesa I know what was wrong now... I drew a wrong picture at first :D
I knew that I was doing this problem correctly. My approach used similar triangles, but I still got a = 1 3 , I just forgot about the implied 1... muted cursing I call shenanigans...
Nice problem! Thanks!
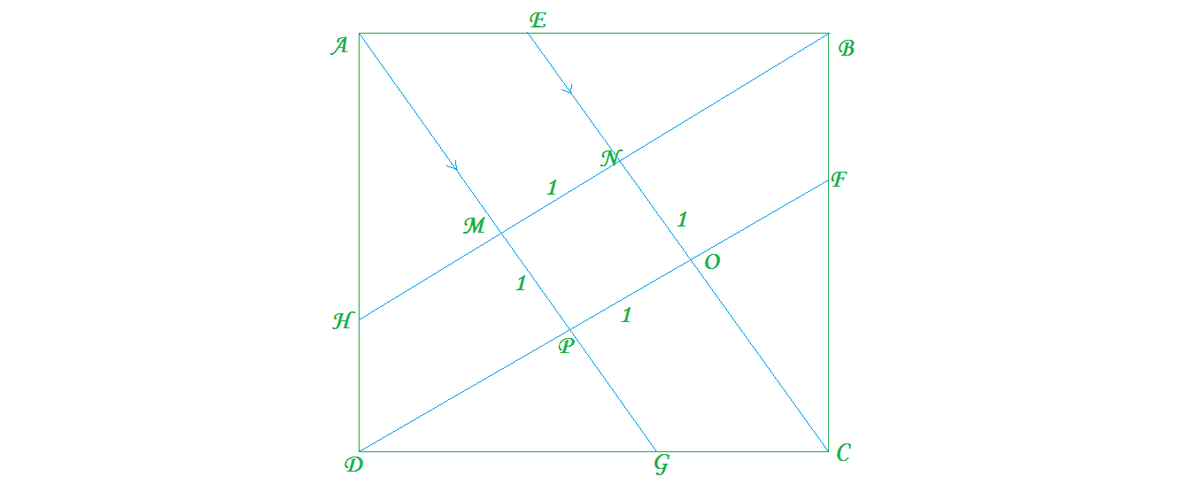
Let the name of the small square formed be MNOP. Clearly, MP || NO .'. AM || EO
In triangle ABM , AM || EO ,
.'. M N B N = A E E B {By the Thales' theorem}
=> 1 B N = 1 2 { .'. MN = 1 and EB= 2AE}
=> BN = 2 Similarly , from △ ADP we get : AM = 2
Now , In △ ABM , AB^2 = BM^2 + AM ^2 {By Pythagoras' theorem}
=> AB^2 = (BN + MN)^2 + AM^2
=> AB^2 = (2+1)^2 + 2^2 {Putting the values which have been found above}
=> AB^2 = 3^2 + 2^2 => AB = √(13)
------------------------------an easy and complete solution by
Vishwash Kumar
Nyc ! Upvoted!
 Square within Trisected square
Square within Trisected square
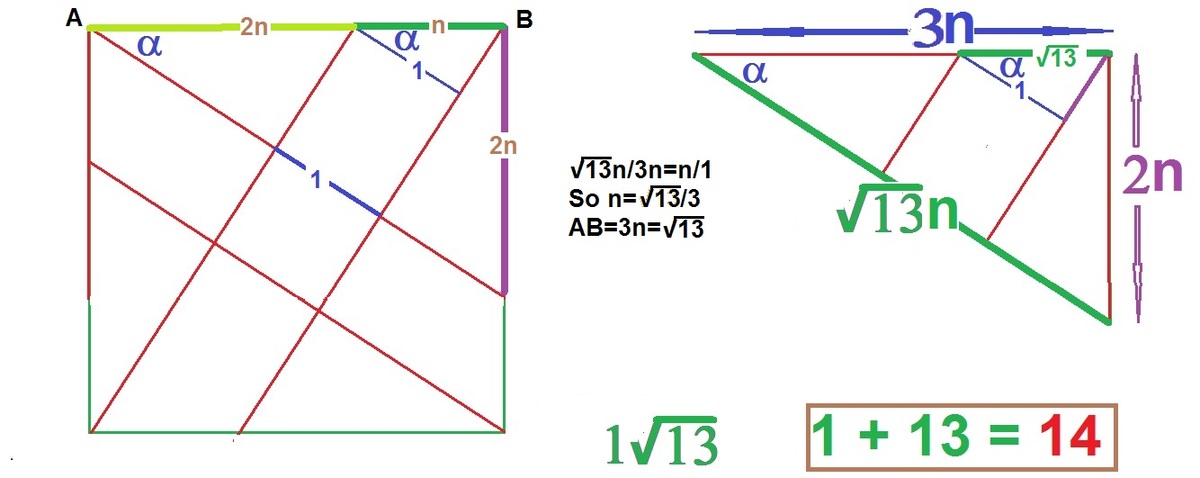
tan α = 3 2 giving cos α = 1 + ( 3 2 ) 2 1 = 1 3 3
Let AB = 3a giving AE = a and A E cos α = A E 1 3 3 = 1 3 A B = 1
A B = 1 3
Surprisingly we think in the same direction again !!.
Log in to reply
As they say, an apple never falls too far from the tree. Same applies to a teacher and student sir! By the way, I had marked a geometry problem based on/solvable using cognate linkages. Not sure if Brilliant forwards messages marked in a solution. If not I can send you the link.
Log in to reply
Messages marked in a solution can be read only when we enter the discussion page. Since I am trying to solve it, I can not see it. Please sent the link.

Let the intersection of A G and B H be I and the intersection of E C and B H be J . Now, we shall set up a coordinate system where A ( 0 , a ) , B ( 0 , 0 ) , C ( a , 0 ) , D ( a , a ) . The side length of the square is thus a . From the question, we have E ( 0 , 3 2 a ) , H ( 3 2 a , a ) , G ( a , 3 1 a ) . From this, we obtain:
Equation of BH: y = 2 3 x Equation of AG: y = − 3 2 x + a Equation of AG: y = − 3 2 x + 3 2 a
Solving for the coordinates of I , J , we get I ( 1 3 6 a , 1 3 9 a ) , J ( 1 3 4 a , 1 3 6 a )
This implies that ∣ I J ∣ = 1 1 3 a = 1 Solving, a = 1 3 So the answer is 1 + 1 3 = 1 4 .