Gimme The Money

Probability Level 2

Two players play a game according to the following rules:

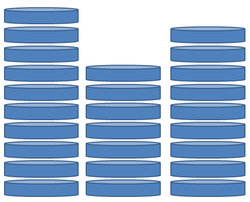
They place three heaps of coins on a table. The first heap has $10$ coins, the second heap has $7$ coins, and the third heap has $9$ coins.
The second player adds another pile of coins on the table, having at most $10$ coins.
The players take turns alternately, starting with the first player. At each move, the player has to remove a positive number of coins from one heap. The player who removes the last coin wins.

It turns out that regardless of the strategy of the first player, the second player always wins with optimal play. How many coins should the second player add in the fourth pile?

The answer is 4.

6 solutions

Yong See Foo
Feb 9, 2014

This is just the game of Nim . If the last pile has $x$ coins, the nim-sum will be $10\oplus 7\oplus 9\oplus x=4\oplus x$ . Since the second player would want this to be zero such that he can guarantee a win, the desired $x$ is $4$ .

Finn Hulse
Feb 9, 2014

I think that you mean coins instead of stones. And "atmost" isn't a word. And I think that you meant to say that you can only remove 1 or 2 coins. I'm not sure if that's what you meant, but if it is, then the answer is 4.

I did change all my "stones" into "coins" before you posted your solution.

Note that I used "at most" as two different words.

When did I say you can remove only $1$ or $2$ coins?

This is not a solution!

Sreejato Bhattacharya - 7 years, 4 months ago

In the second dot point it is still stones.

Yong See Foo - 7 years, 4 months ago

Oops, thanks for noticing it. Fixed!

Sreejato Bhattacharya - 7 years, 4 months ago

I think this problem is a case of NIM game.

Dino Hà - 7 years, 2 months ago

Shib Shankar Sikder
Mar 20, 2014

The player who starts has a winning strategy if and only if the bit-wise 1-modulo sum of the total number of elements is not zero. Otherwise the other player has a winning strategy. Here the player who plays 2nd controls the stacks. So he will make the modulo sum 0 so that he has a winning strategy. 10 XOR 7 XOR 9 = 4 If he puts 4 in the new stack it makes the total modulo sum 0. Then he cannot lose if he does not make a mistake.

this is wrong, a player can remove the entire pile if he wants to. Suppose P1 removes first pile, then the second player removes either a pile or not. If he removes a complete pile, P1 will remove coins leaving some coins in the pile. If P2 removes another pile, then P1 is left with only one pile , which gives him win.If he does not remove the pile, he will try to get both piles down to 1 coin each, which is not always possible, because if P1 gets it, he'll win.

If P2 does not remove the second pile, P1 will remove a pile following the same strategy as above after that to win.

vipul soni - 7 years, 1 month ago

Jam M
Apr 23, 2021

10: 8 2

7: 4 2 1

9: 8 1

x: 4

If player 2 is to win with optimal play, then the starting configuration must have a nim sum of 0. This is achieved if player 2 adds 4 coins to the last pile.

Shamik Banerjee
Feb 16, 2014

Theorem. In a normal Nim game, the player making the first move has a winning strategy if and only if the Nim-Sum of the sizes of the heaps is nonzero. Otherwise, the second player has a winning strategy.

Nim is a mathematical game of strategy

The question is badly phrased. Can a negative number be removed from the heap? Also, what is to stop the first player from removing all the coins from one heap at one go. There is no stipulation that he could not do so, or there are no restrictions on the number of coins he could remove from a heap.

hilton tottaram - 7 years, 3 months ago

Please read the question carefully. I did mention that "at each move a player has to remove a positive number of stones". Regarding your second query, a player has the permission to remove all coins from one heap, but that doesn't imply that he wins. You have to remove all coins from each of the four piles to win.

Sreejato Bhattacharya - 7 years, 3 months ago

Thanks.

hilton tottaram - 7 years, 3 months ago

Christopher Liu
Feb 16, 2014

This is a game of Nim. And can be solved using the nimber. The nimber is the xor of all the binary representations of the piles. In this case, 10 = 1010, 9 = 1001, 7 = 111. So we want to add a pile such that it is 1010 xor 1001 xor 111 = 100 = 4.

Gimme The Money

The answer is 4.

6 solutions

0 pending reports