Trojan Horses
Logic
Level
3
Whose move is it now?
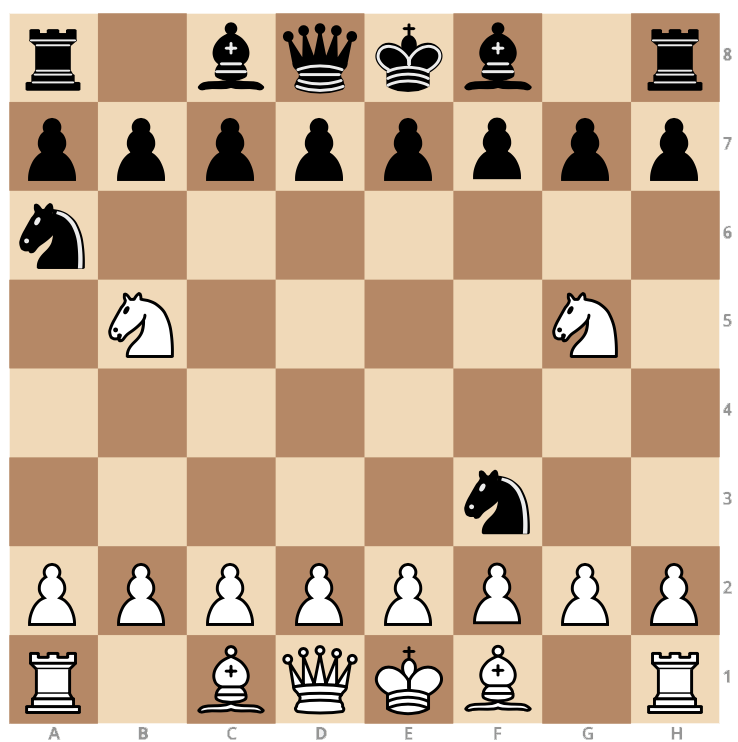
White to move
Black to move
Cannot be determined
This is an impossible position
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Chess Puzzles
Looking at the board, we see that none of the pawns have moved. This implies that none of the bishops have moved, and therefore the kings and queens haven't moved either. The only pieces that might have moved are the knights and the rooks.
The knights' and the rooks' positions tell us that it should be Black's turn to play (proof given below). However, the knight at f3 is giving a check to the white king. It is not possible for White to play a move and still remain in check after the move. Therefore the given position is impossible. □
Proof: Let the white squares have the value '0', and the black squares value '1'. Observe the four squares occupied by the white knights and rooks. Let the sum of these squares be S W . Similarly, let the sum of the four squares occupied by the black rooks and knights be S B .
When the game starts, we see that both S W and S B are even, and it is White's turn to move. When white makes a move, the parity of S W changes. S B and S W have different parity, and it is Black's turn to move.
Whenever a player makes a move, its parity will change. This is because the knight moves to a square opposite in color to its initial square. The rooks are trapped by the pawns and the bishops, so they can only move to a square of opposite color. Either way, change in parity is guaranteed when a move is made.
From this, we can conclude:
We see that in the given position, S W is even, and S B is odd. Their parities are different; this means that it should be Black's turn to move.