Trotter the Turkey's Acorn Walk

Logic Level 1

Trotter the Turkey wants to collect all of the acorns while avoiding the pesky squirrels.

Can Trotter do this without visiting any square twice?

Yes No

Jason Dyer by Jason Dyer

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

8 solutions

Wind Quotidian
Nov 17, 2017

One way to solve the problem.

116 Helpful 0 Interesting 2 Brilliant 0 Confused

Moderator note:

Assuming the problem is restricted to a) just horizontal and vertical movement and b) the turkey has to return to the starting point, this is akin to the problem of the wazir tour . The chess piece of the wazir is like a rook, but can only move one square horizontally or vertically at a time. The purpose of a wazir tour is to visit every square on the board and return to the start. There are, for example, 374 wazir tours on an 8x8 chessboard. Here is a sampling:

Source, George Jelliss .

I suspect that this is the only possible path, (irrespective of direction).

Brian Charlesworth - 3 years, 6 months ago

Log in to reply

@ Brian: No. For example you could go left,up,right,up,left in the beginning. (But Trotter would not end up at his starting point.)

Alexander Zwink - 3 years, 6 months ago

Log in to reply

Ah, ok, good point. For some reason I had assumed that Trotter had to return to his starting point, but that is not in fact a requirement.

Brian Charlesworth - 3 years, 6 months ago

It's doesn't specify that you can not go diagonally

Rosa Bartok - 3 years, 6 months ago

Log in to reply

It does, for the first version of the question. It would be more ways to go when we can go diagonally, though! :) Thanks for pointing that out.

Wind Quotidian - 3 years, 6 months ago

It doesn't specify that you can't jump over squares either... ;-)

Rune Knappskog - 3 years, 6 months ago

Why are the squirrel there?

Atish Behera - 3 years, 6 months ago
Luke Lowery
Nov 26, 2017

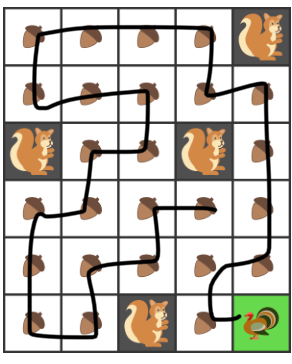
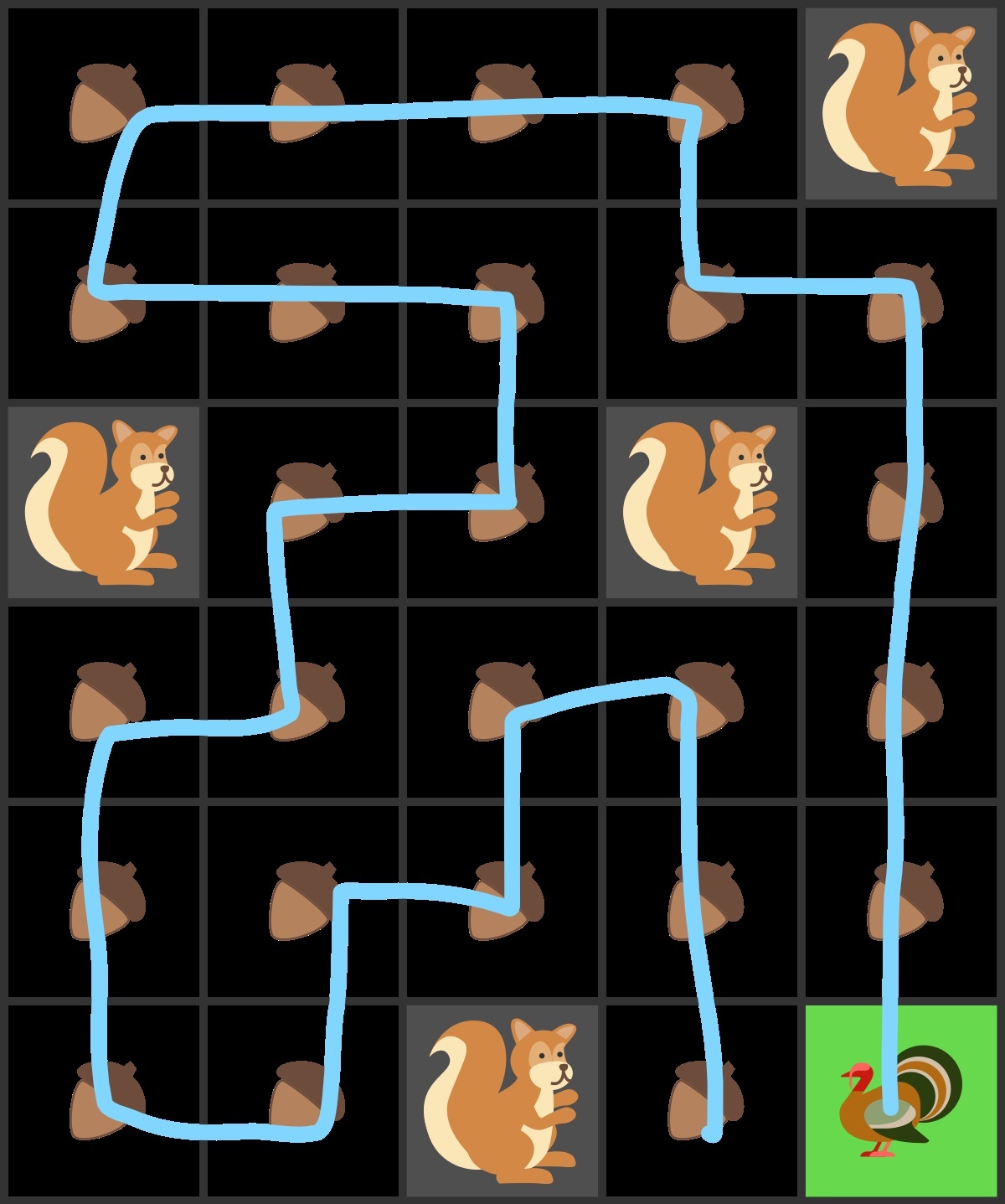
This is a solution so that the turkey avoids all squirrels, gets all the acorns, and returns home. This is one alternative solution where the turkey avoids all squirrels, gets all the acorns, but does not return home.

Difference in each solutions is a few changes to starting and ending moves, main path remains the same.

28 Helpful 0 Interesting 0 Brilliant 0 Confused

I thought that Trotter couldn't go around the squirrels and so I thought, It's not possible. I think what works best for this is using logical reasoning and drawing a diagram. I think I should have read the instructions more carefully and draw a close up diagram. I would rate this problem a 1 because it's fairly easy, I just needed to read the instructions more carefully. I felt like it was going to be easy but I didn't read the instructions carefully enough.

Lucia Tiberio - 3 years, 6 months ago

Seems fair.. however..turkey shall not return home...bcz no square is to be visited twice as per question. Thought?

piyush upadhyay - 3 years, 4 months ago
Sachin Rawat
Nov 26, 2017

16 Helpful 0 Interesting 0 Brilliant 0 Confused

the one that sachin rawat did the same thing i did

Kali Muller - 3 years, 6 months ago

I worked out a solution then accidentally clicked "no". Now I am officially stupid. There appears to be no way to undo this. (Hint to the developers: make it easier to change, because I felt like closing it, which would lose customers).

Erik Bentham - 3 years, 6 months ago

Yes if you assume that 2 squares connected by their corner are not adjacent to each other... otherwise it's a no !

Cédric Poncet-Montange - 3 years, 6 months ago

solved this in 10 secs first try so easy

Kage1128 . - 3 years, 6 months ago

I see this as a graph problem, I am quite weak at graph algorithms for now, can anyone tell me what algorithm could solve this problem, finding a path the goes through each and every node only once?

Eyad Hajja - 3 years, 6 months ago

dear Wrong pattern was shown according to the solution it had one acron on the left hand top above the squirrel

ajay kumar varma varma - 3 years, 6 months ago
Charlotte Cooper
Nov 27, 2017

I think you can solve this as a decision maths problem where the grid is a graph, the acorns are the vertices and the edges are the possible paths the turkey could use to get from one to the next - you end up with an even number of vertices of an odd degree proving at least that it can be done!

2 Helpful 0 Interesting 0 Brilliant 0 Confused

How would you construct a graph to prove a solution exists?

michael greene - 3 years, 6 months ago

I think you mixed up your concepts.

We're looking for a hamiltonian path . Unfortunately, this is NP-hard, as compared to finding a eulerian path .

Calvin Lin Staff - 3 years, 6 months ago
Alex Wang
Nov 28, 2017

25 squares = odd number hamiltonian paths are possible on odd numbers think about a chessboard. if there is even squares, then start and end squares are different colors, so if they are same, then it cant exist

1 Helpful 0 Interesting 0 Brilliant 0 Confused

You’re the real mathematician here. You show that a solution exists, and then you leave it to the engineers to actually find the solution!

Jordan Fischer - 3 years, 6 months ago

I found this

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Frank Kelley
Dec 2, 2017

When deciding on a path, I asked the question for each move: will this move create a deadend block? Sounds tedious, but worked very well because it helped me see pathways down the way which saved time.

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Kiichi Takeuchi
Dec 2, 2017

First I quickly checked that if there are any dead end single cell which you have to go backwards unless it’s the last visit but no such a spot. Then I tried a pattern that proved some pics like below.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...