Find the shortest path

Geometry Level 3

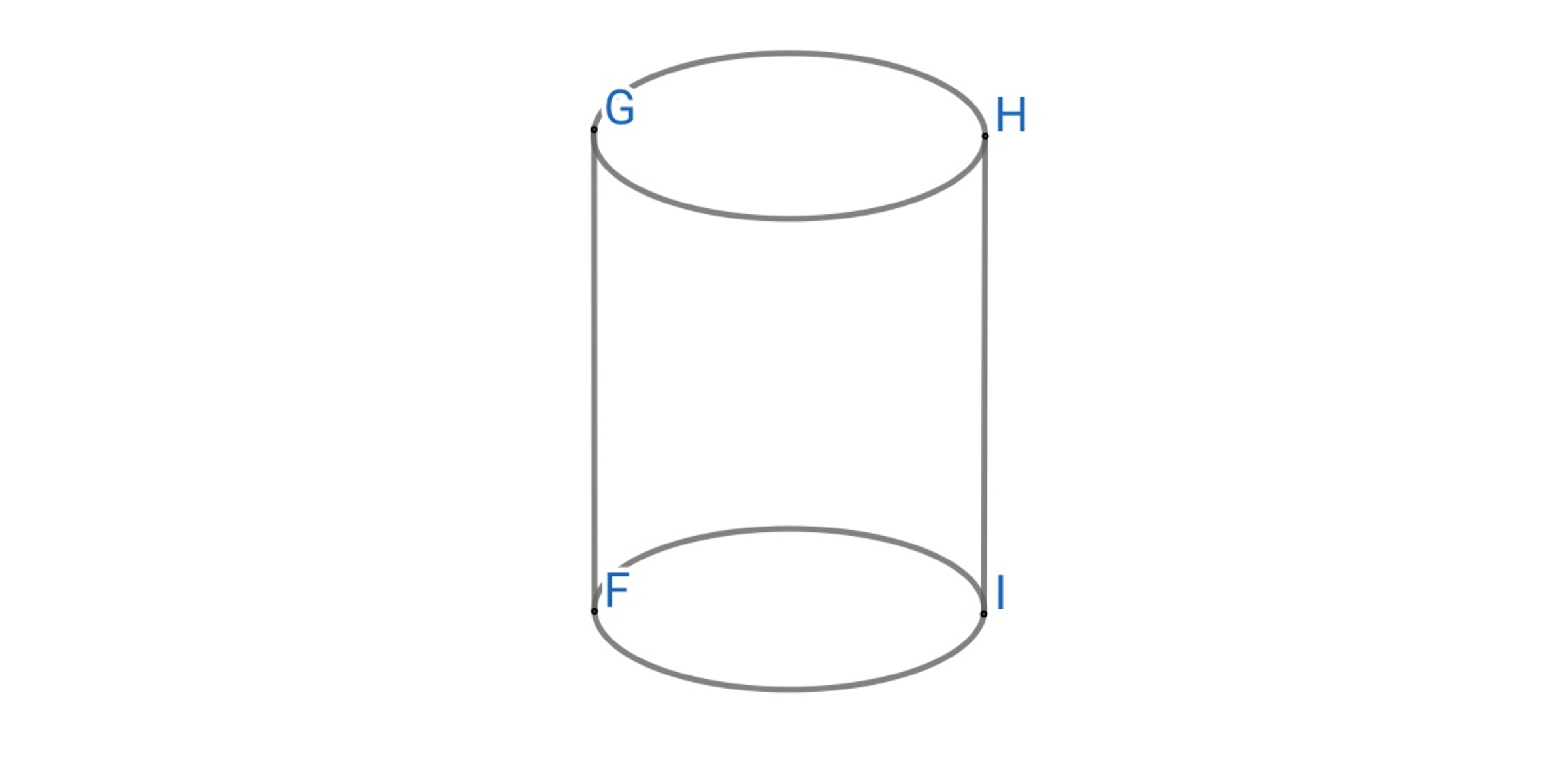
There’s a cylinder as follows. Its two undersides are solid surfaces. When putting it on the table, its base circumference is $48$ and its height is $7$ .

True or false? If an ant wants to go from $F$ to $H$ (Crawling on the surface of the cylinder), its shortest route is $25$ .

False True

1 solution

Edward Christian
Aug 15, 2019

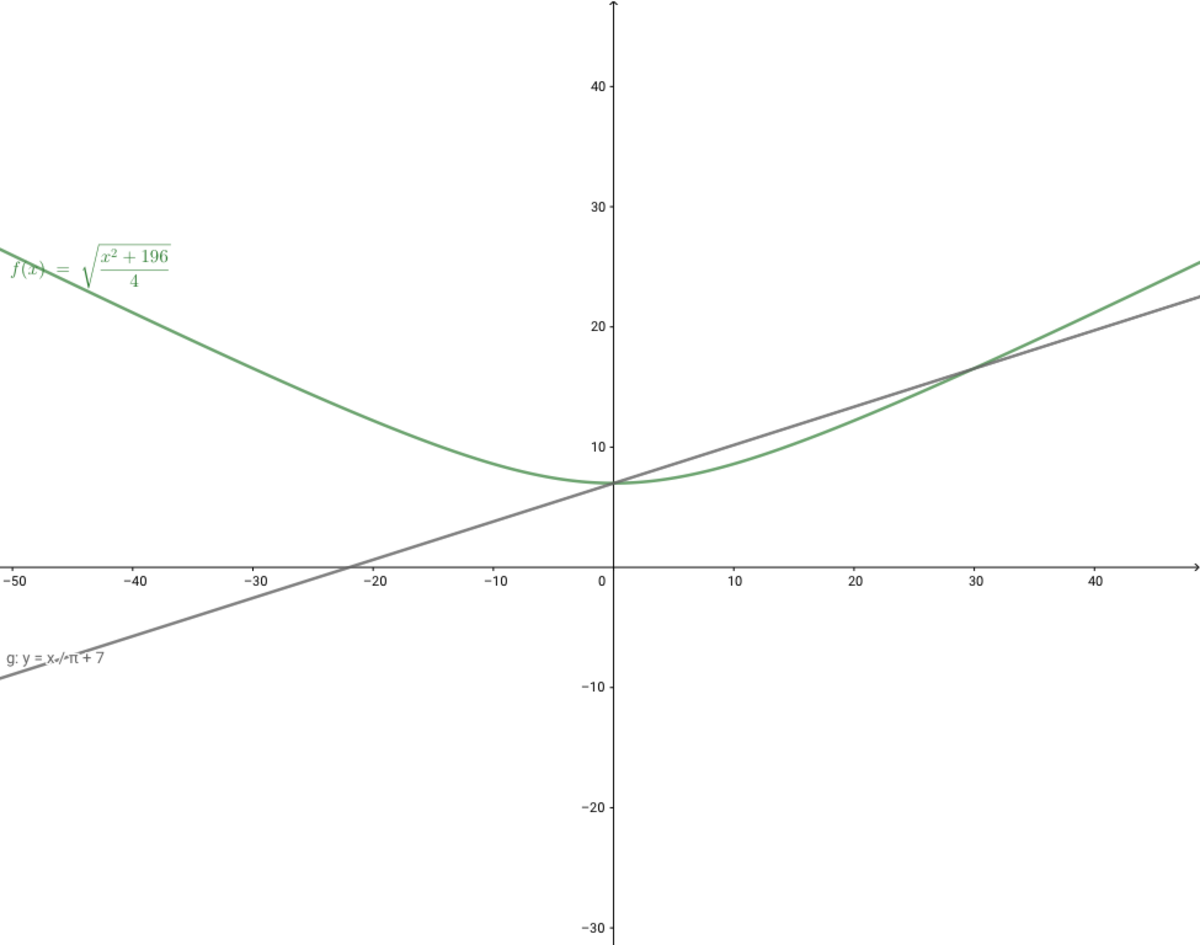
Now we have 2 routes. One is $FH$ , the other is $FG-GH$ . We can get $FH=\sqrt{(\dfrac{48}{2})^2+7^2}=25$ . The other route $FG-GH=\dfrac{48}{\pi}+7\approx 22.3<25$ . So the answer is flash.

NOTE: To further explore, for a cylinder with height $7$ and base circumference $x$ , we construct the function $f(x)=\sqrt{(\dfrac{x}{2})^2+7^2}=\sqrt{\dfrac{x^2}{4}+\dfrac{49\times 4}{4}}=\sqrt{\dfrac{x^2+196}{4}},g(x)=\dfrac{x}{\pi}+7$ and graph it,

I'm not doubting your solution, but how come we consider FG - GH to be a possible path in this case?

Deva Craig - 1 year, 9 months ago

it's just another way to get from F to H

Ishaan Ivaturi - 1 year, 9 months ago

This question really punked me as expected. I calculated ONE of the paths to be 25. But I got punked... Great question

Krishna Karthik - 1 year, 4 months ago

Find the shortest path

1 solution

0 pending reports