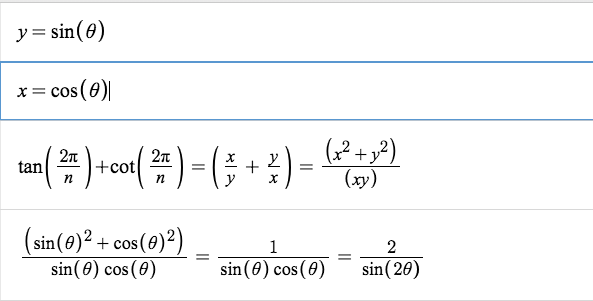True Polynomial Hunting

This was my approach: The tan and the cot can be expressed as ratios of $sin(A)$ and $cos(A)$ . When summing, for some angle $A=$ $\frac{2π}{n}$ , $tan(A) + cot(A) =$ $\frac{1}{sin(2A}$ . Since $\frac{2}{sin(2A)}$ can be irrational and cannot always be expressed as operations with radicals, the polynomial that has $\frac{2}{sin(2A)}$ as a root does not always have a conjugate for all possible values of $A$ . If it does have a conjugate, the coefficients would be rational as the radicals would cancel out. As a result, the polynomial does not always have rational coefficients, so $tan(A) + cot(A)$ is not always algebraic.

My work:

While it can be easily seen that such expression may be derived from $\zeta=e^{ \dfrac{2\pi i}{n}}$ , it will fail to produce algebraic numbers when $n = 0$ , $n=1$ and $n=4$ , as it will yield undefined expressions.