Truncated Right Triangular Prism
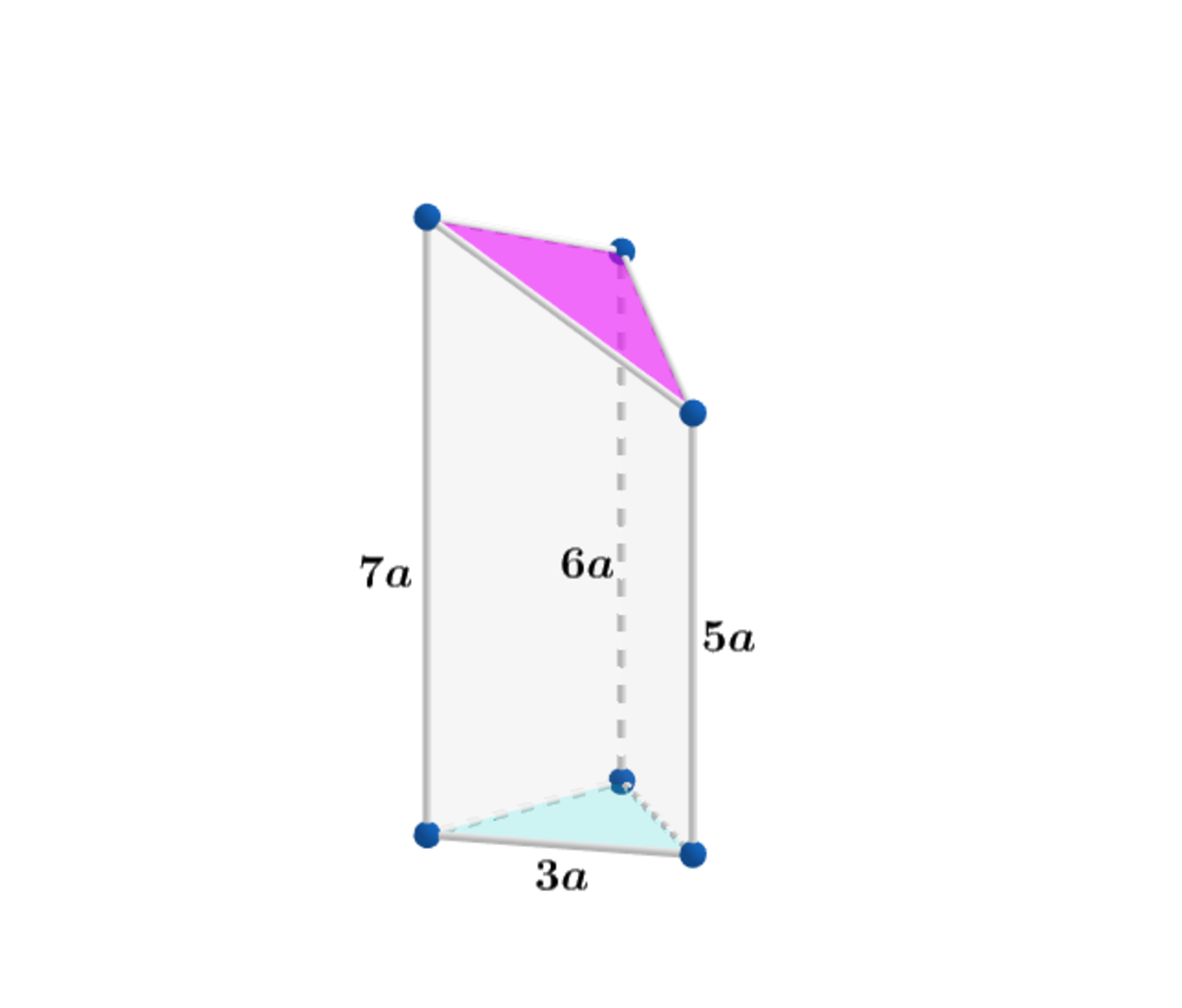
In the truncated right triangular prism above, the base is an equilateral triangle with side length 3 a and the lateral edges have lengths 7 a , 5 a and 6 a .
Let V and A s represent the volume and the total surface area of the truncated right triangular prism above. If the value of a for which the ratio A s V = 7 2 + 3 9 − 3 3 can be expressed as a = β β α ( λ + ω γ ) , where α , β , λ , ω and γ are coprime positive integers, find α + β + λ + ω + γ .
The answer is 489.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Volume of the Solid
V = Base area × Average height of the solid = 4 3 ( 3 a ) 2 × 3 5 a + 6 a + 7 a = 2 2 7 3 a 3
Surface Area of the Solid is the sum of:
- the base area 4 3 ( 3 a ) 2 = 4 9 3 a 2
- the area of the three vertical sides 3 a ( 2 5 a + 6 a + 2 6 a + 7 a + 2 7 a + 5 a ) = 5 4 a 2
- the area of the top triangle: The top triangle is an isosceles triangle with equal sides of length 1 2 + 3 2 a = 1 0 a and base of length 2 2 + 3 2 a = 1 3 a . Therefore, a height h = 1 0 − 4 1 3 a = 2 3 3 a and an area A = 2 1 × 1 3 a × 2 3 3 a = 4 3 3 9 a 2
Therefore A s = 4 2 1 6 + 3 3 9 + 9 3 .
And we have:
A s V 2 1 6 + 3 3 9 + 9 3 5 4 3 a 7 2 + 3 9 + 3 3 1 8 3 a ⟹ a = 7 2 + 3 9 − 3 3 = 7 2 + 3 9 − 3 3 = 7 2 + 3 9 − 3 3 = 1 8 3 ( 7 2 + 3 9 ) 2 − ( 3 3 ) 2 = 1 8 3 5 1 9 6 + 1 4 4 3 9 = 3 3 8 6 6 + 2 4 3 9 = 3 3 2 ( 4 3 3 + 1 2 3 9 )
Therefore α + β + λ + ω + γ = 2 + 3 + 4 3 3 + 1 2 + 3 9 = 4 8 9 .
Using the pythagorean theorem we have:
A B = 1 3 a and B C = 1 0 a = A C
To find the area A △ A B C we use Heron's formula obtaining:
s = 2 1 3 + 2 1 0 a ⟹ A △ A B C = 4 3 3 9 a 2
For the area of the trapezoidal faces we have:
A A E G B = 1 8 a 2
A B G F C = 2 3 3 a 2
A A E F C = 2 3 9 a 2
and
A △ E G F = 4 9 3 a 2
⟹ A s = 4 3 ( 7 2 + 3 9 + 3 3 ) a 2
and
V = 4 9 3 ( 3 7 + 6 + 5 ) a 3 = 4 5 4 3 a 3
⟹ A s V = 7 2 + 3 9 + 3 3 1 8 3 a = 7 2 + 3 9 − 3 3 ⟹
a = 1 8 3 7 2 2 + 1 4 4 3 9 + 3 9 − 2 7 = 3 3 2 ( 4 3 3 + 1 2 3 9 ) =
β β α ( λ + ω γ ) ⟹ α + β + λ + ω + γ = 4 8 9 .