Truncated Square Pyramids
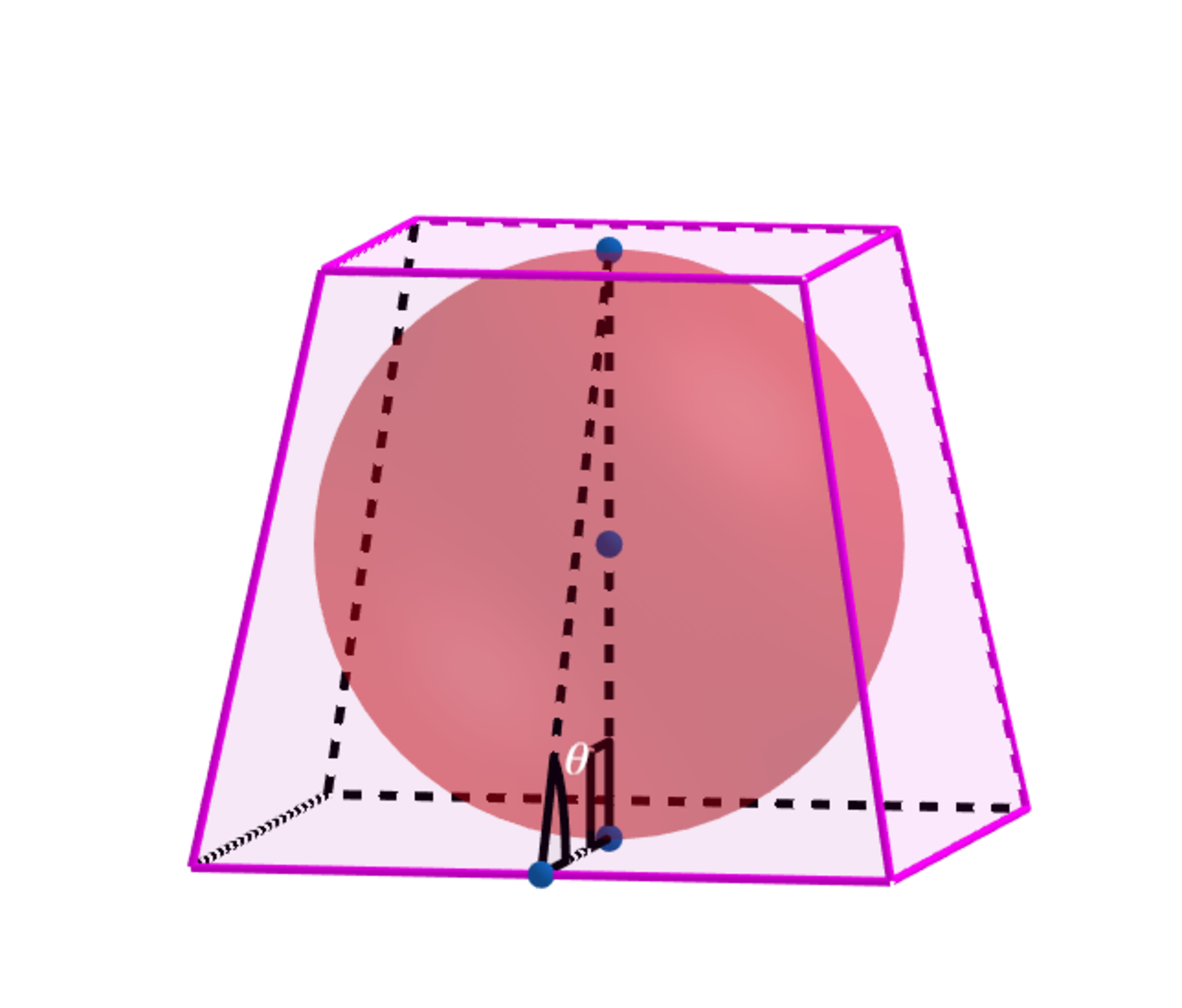
In the diagram above, a sphere is inscribed in a truncated square pyramid such that the volume of the truncated square pyramid is twice the volume of the inscribed sphere.
Find the measure of the angle (in degrees) made with the larger base.
Note: If is the length of a side of the square base and is the height of the square truncated pyramid, then .
I.E; is not the slant height angle.
The answer is 58.91655379.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Using the fact that tangents to a circle from an outside point are congruent we obtain the diagram above.
The height h of the truncated square pyramid is h = 2 r
Using right △ A B C we have:
( w + m ) 2 = ( w − m ) 2 + 4 r 2 ⟹ w 2 + 2 w m + m 2 = w 2 − 2 w m + m 2 + 4 r 2 ⟹ 4 w m = 4 r 2 ⟹ r 2 = w m ⟹
r = w m .
The volume of the inscribed sphere V s = 3 4 π ( w m ) 2 3
and
The volume of the truncated cone is V T = 3 2 π ( 4 w 2 + 4 w m + 4 m 2 ) ( w m ) 2 1
= 3 8 π ( w 2 + w m + m 2 ) ( w m ) 2 1
V T = 2 V s ⟹ w 2 + w m + m 2 = π w m ⟹ w 2 − ( π − 1 ) w m + m 2 = 0 ⟹ w = ( 2 π − 1 ± ( π − 1 ) 2 − 4 ) m
Since m w > 1 we choose w = ( 2 π − 1 + π 2 − 2 π − 3 ) m
and h = 2 w m = ( 2 2 π − 1 + π 2 − 2 π − 3 ) m
⟹ tan ( θ ) = w h = π − 1 + π 2 − 2 π − 3 2 2
⟹ θ ≈ 5 8 . 9 1 6 5 5 3 7 9 ∘