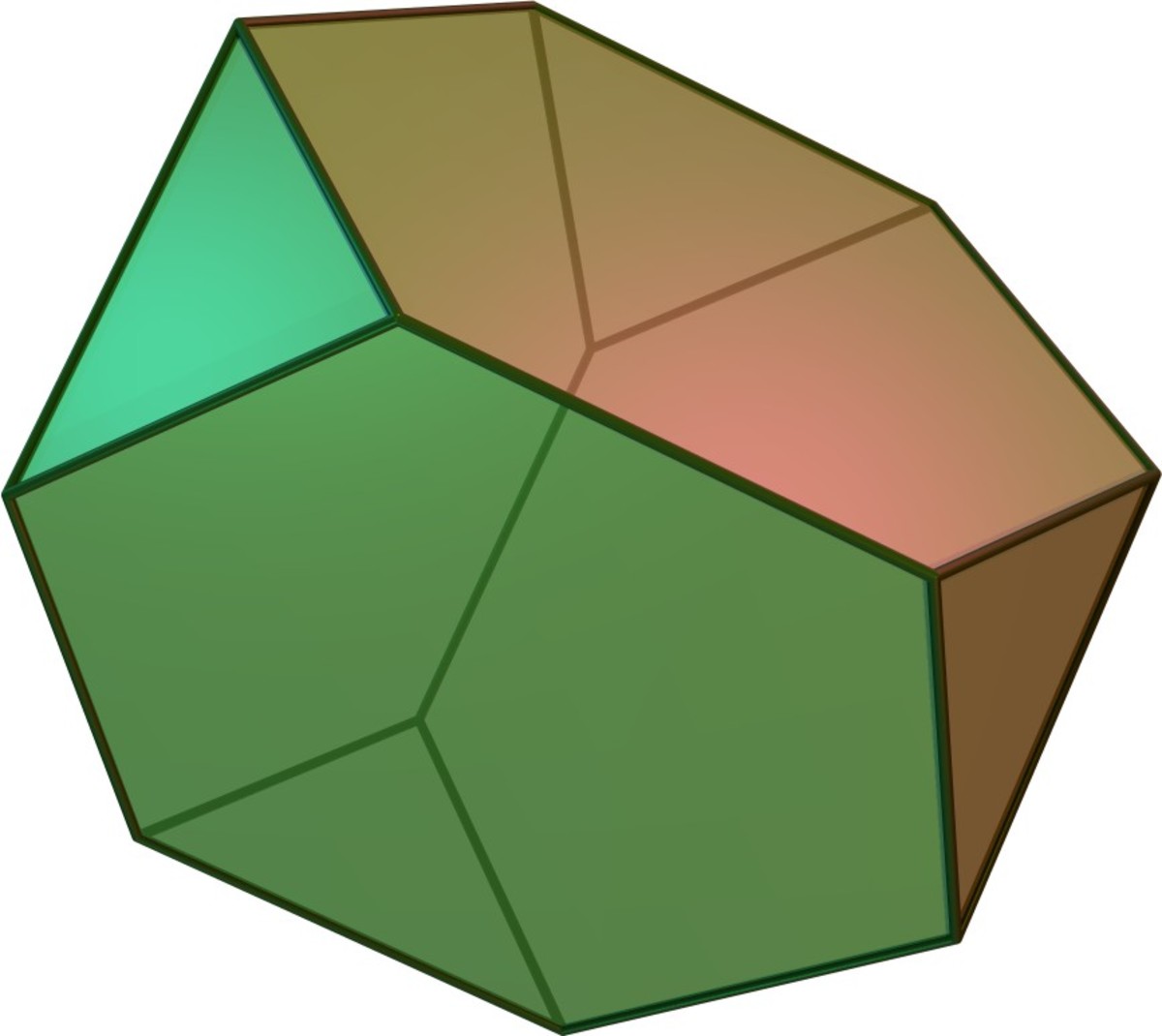
Truncated!

Geometry Level 3

If the number of hexagonal faces in a truncated tetrahedron is a a and the number of triangular faces is b b , Find the value of

2 a + 2 b \large{2^{a}+2^{b}}


The answer is 32.

Md Zuhair by Md Zuhair , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

X X
May 15, 2018

2 4 + 2 4 = 32 2^4+2^4=32

4 Helpful 0 Interesting 0 Brilliant 0 Confused
Blan Morrison
May 11, 2018

For every face on the original tetrahedron, there is a hexagonal face on the truncated version. For every vertex on the original version, there is a triangular face on the truncated version.

4 faces = 4 hexagons = a 4 \text{ faces} = 4 \text{ hexagons} = a 4 vertices = 4 triangles = b 4 \text{ vertices} = 4 \text{ triangles} = b 2 4 + 2 4 = 2 × 2 4 = 2 5 = 32 2^4+2^4=2\times 2^4=2^5=\boxed{32}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

But, why is this a Chemistry question?

Aryan Sanghi - 3 years ago

Log in to reply

@aryan sanghi I agree with you.....!! But now it is tagged under Geometry section....

Aaghaz Mahajan - 3 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...